O retângulo possui quatro lados e todos os ângulos internos medindo 90°. Essa forma geométrica está muito presente no cotidiano, como na face de caixas e nas paredes.

O retângulo é uma das figuras planas mais presentes no nosso cotidiano. Podemos observar caixas, paredes, mesas e vários outros objetos que possuem faces retangulares. O retângulo é um polígono de quatro lados e recebe esse nome por possuir todos os ângulos internos retos, ou seja, medindo 90°. Para calcular a área de um retângulo, multiplicamos a sua base pela sua altura. Já o perímetro é igual à soma de todos os seus lados.
Essa forma é composta por 4 vértices e 4 lados. Em um retângulo, podemos traçar duas diagonais, e o comprimento dessas diagonais é calculado utilizando o teorema de Pitágoras. Existem também o trapézio retângulo e o triângulo retângulo, que recebem tais nomes por possuírem ângulos retos.
Leia também: Soma dos ângulos internos de um polígono — que expressão matemática pode ser usada?
O retângulo é um polígono que possui os 4 ângulos internos retos.
Para calcular a área de um retângulo, multiplicamos a sua base e a sua altura.
O perímetro de um retângulo é igual à soma de todos os seus lados.
Em um retângulo, podemos traçar duas diagonais.
A diagonal do retângulo divide o retângulo em dois triângulos, de modo que o teorema de Pitágoras pode ser aplicado.
Se um trapézio possui dois de seus ângulos retos, ele é chamado de trapézio retângulo.
Se dividirmos o retângulo ao meio por uma das suas diagonais, encontramos um triângulo retângulo.
As formas geométricas nos cercam em nosso cotidiano, e o retângulo é uma forma bastante comum. O retângulo possui quatro ângulos internos retos, ou seja, os seus ângulos internos medem 90°.

Existem outros elementos importantes em um retângulo, além dos seus 4 ângulos retos. São eles:
os seus vértices;
os seus lados;
as suas diagonais.
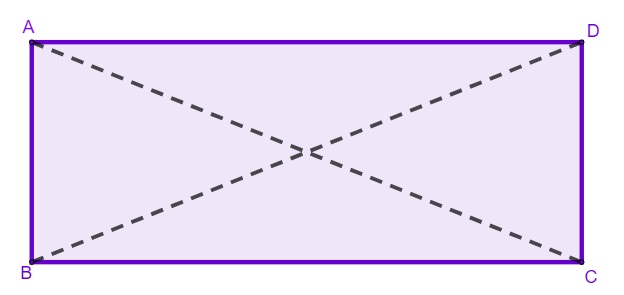
Como pode ser observado na figura acima,
A, B, C e D são os vértices do retângulo;
AB, AD, BC e CD são os lados do retângulo;
AC e BC são as diagonais do retângulo.
O retângulo possui lados opostos paralelos, o que faz com que ele seja classificado como um paralelogramo. Por ser um paralelogramo, possui propriedades importantes. São elas:
lados opostos congruentes;
ângulos internos que medem 90°;
ângulos externos que também medem 90°;
diagonais congruentes;
diagonais que se encontram no ponto médio.
Saiba mais: Quadrado — figura que pertence ao conjunto dos quadriláteros
Existem fórmulas importantes envolvendo os retângulos, utilizadas para calcular a medida da sua área, do seu perímetro e de suas diagonais.
Para calcular a medida da superfície de um retângulo, ou seja, a sua área, realizamos a multiplicação da base pela altura:
\(A\ =\ b\ \cdot h\ \)
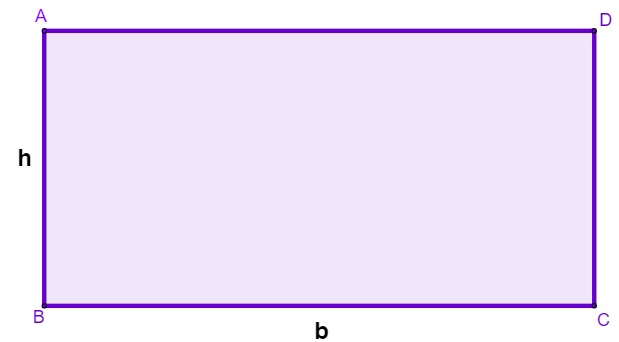
b ➜ base do retângulo
h ➜ altura do retângulo
Importante: Note que em um retângulo a altura coincide com o comprimento dos lados AB e DC.
Um terreno possui formato retangular com base medindo 7,5 metros e altura igual a 5 metros. Qual é a área desse terreno?
Resolução:
Para calcular a área, basta realizar a multiplicação entre 7,5 e 5:
\(A\ =\ 7,5\ \cdot5\)
\(A=37,5m^2\)
Saiba também: Áreas de figuras planas — as fórmulas de acordo com cada forma geométrica
O cálculo do perímetro de qualquer figura plana é dado pela soma de seus lados. Em um retângulo, como os lados opostos são congruentes, podemos calcular o perímetro utilizando a fórmula:
\(P=2\left(b+h\right)\)
Qual é o perímetro de um terreno retangular que possui lados medindo 7,5 metros e 5 metros?
Resolução:
Sabemos que o perímetro é a soma de todos os lados, então temos que:
\(P=2\ \left(7,5+5\right)\)
\(P\ =\ 2\ \cdot12,5\ \)
\(P\ =\ 25\ m\)
Ao traçar a diagonal de um retângulo, percebemos que ela divide o retângulo em dois triângulos. A partir daí, é possível aplicar o teorema de Pitágoras no triângulo retângulo formado.
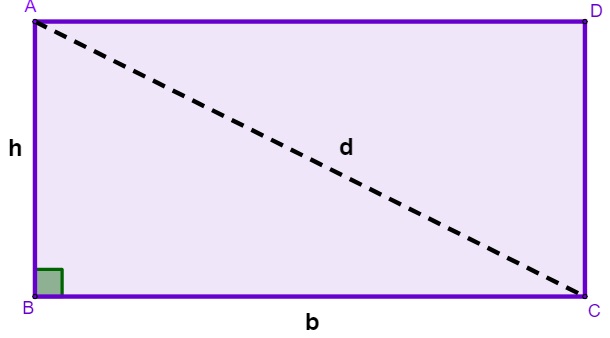
Qual é a diagonal de um retângulo que possui base medindo 8 cm e altura de 6 cm?
Resolução:
Calculando a diagonal:
d² = 8² + 6²
d² = 64 + 36
d² = 100
d = \(\sqrt{100}\)
d = 10 cm

O trapézio é um polígono que possui quatro lados, sendo que dois deles são paralelos e os outros dois, não. Um trapézio é chamado de trapézio retângulo quando possui dois de seus ângulos retos.
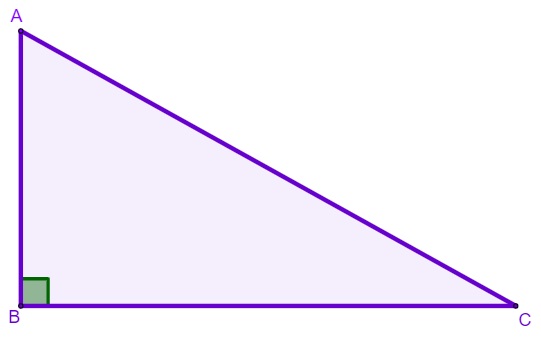
O triângulo retângulo é estudado a fundo na Geometria Plana, tornando possível o desenvolvimento de teoremas importantes, como o teorema de Pitágoras, além dos estudos da Trigonometria. Como vimos anteriormente, se dividirmos o retângulo ao meio por uma das suas diagonais, encontraremos um triângulo retângulo, pois o triângulo é considerado triângulo retângulo quando ele possui um ângulo interno de 90°.
Questão 1
Na fazendo do Seu João, uma área no formato de retângulo foi separada para o cultivo de milho. Antes de plantar, Seu João decidiu cercar essa área com 4 voltas de arame farpado, para dificultar a entrada de animais e pessoas. Sabendo que a área de cultivo possui 22 metros de largura e 18 metros de comprimento, qual é a quantidade mínima de arame necessária para cercar a região?
A) 80 metros
B) 160 metros
C) 240 metros
D) 320 metros
Resolução:
Alternativa D
Primeiramente, calcularemos o perímetro dessa região:
\(P=2\cdot\left(22+18\right)\)
\(P\ =\ 2\cdot40\ \)
\(P\ =\ 80\ m\ \)
Sabendo que o perímetro é de 80 metros, multiplicaremos 80 por 4, já que serão dadas 4 voltas:
\(80\ \cdot4\ =\ 320\ m\ \)
Questão 2
Qual é a área do retângulo a seguir, sabendo que seus lados foram medidos em metros?
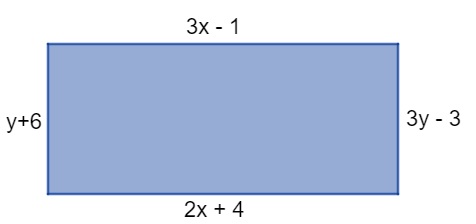
A) 45 m²
B) 180 m²
C) 240 m²
D) 252 m²
Resolução:
Alternativa D
Sabemos que os lados opostos são iguais. Assim, para encontrar o valor de x, temos:
\(3x\ -\ 1\ =\ 2x\ +\ 4\ \)
\(3x\ -\ 2x\ \ =\ 4\ +\ 1\ \)
\(x\ =\ 5\ \)
Agora, encontraremos o valor de y:
\(3y\ -\ 3\ =\ y\ +\ 6\ \)
\(3y\ -\ y\ =\ 6\ +\ 3\ \)
\(2y\ =\ 9\)
\(y=\frac{9}{2}\)
\(y\ =\ 4,5\ \)
Para calcular a área, é necessário encontrar o comprimento dos lados. Portanto, substituiremos na equação da base o valor encontrado pra x e na da altura o valor encontrado pra y.
\(2x\ +\ 4\ =\ 2\ \cdot10\ +\ 4\ =\ 20\ +\ 4\ =\ 24\ \)
\(y\ +\ 6\ =\ 4,5\ +\ 6\ =\ 10,5\ \)
Calculando a área, temos que:
\(A\ =\ b\ \cdot h\)
\(A\ =\ 24\ \cdot10,5\ \)
\(A=252\ m^2\)