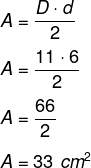Área de uma figura plana é a medida da superfície dessa figura. Para fazer o cálculo de área de uma figura plana, utilizamos a fórmula de acordo com a forma geométrica.
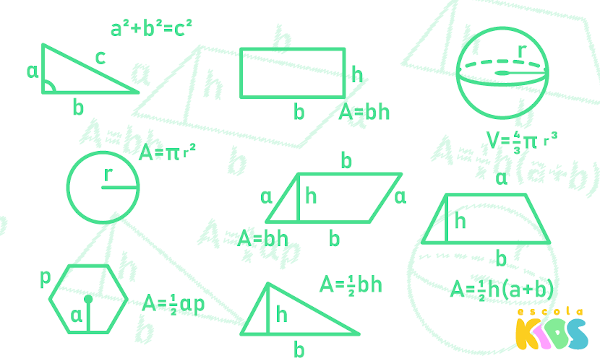
A área de uma figura plana é a medida da superfície dessa figura. O cálculo da área é de grande importância para resolver determinadas situações envolvendo figuras planas. Cada uma das figuras planas possui uma fórmula específica para o cálculo de área. A área é estudada na geometria plana, já que calculamos a área de figuras bidimensionais.
Leia também: Diferença entre circunferência, círculo e esfera
O triângulo é o polígono mais simples da geometria plana, pois é composto por 3 lados e 3 ângulos, sendo o polígono com menor número de lados. Como o nosso objetivo é calcular a área do triângulo, é importante saber reconhecer sua base e altura.
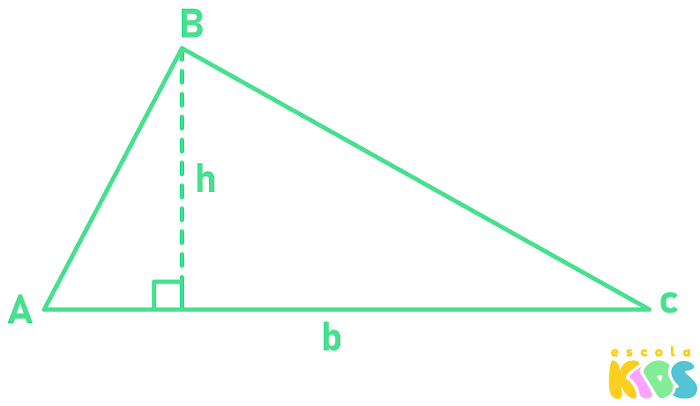
A área do triângulo é igual ao produto entre a base e a altura dividido por 2.
![]()
b → comprimento da base
h → comprimento da altura
Exemplo:
Qual é a área de um triângulo cuja base mede 10 cm e altura é de 9 cm?
Resolução:
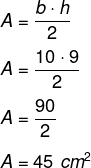
O quadrado é um polígono que possui 4 lados. É considerado um polígono regular por possuir todos os lados e ângulos congruentes entre si, ou seja, os lados possuem a mesma medida, assim como os ângulos. O elemento mais importante no quadrado para o cálculo da área é o seu lado.
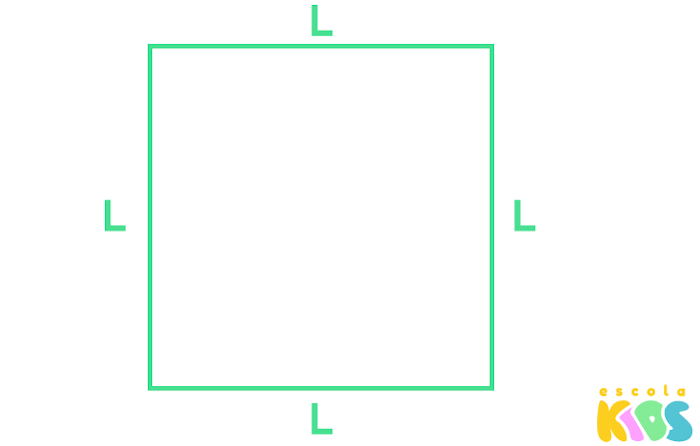
Em um quadrado qualquer, para calcular a sua área, é necessário conhecer a medida de um dos seus lados:
A = l2
l → comprimento do lado
Exemplo:
Qual é a área de um quadrado que possui lados com 6 cm de comprimento?
Resolução:
A = l2
A = 62
A = 36 cm2
O retângulo recebe esse nome por possuir ângulos retos. É o polígono de 4 lados que possui todos os ângulos congruentes e medindo 90°. Para calcular a área do retângulo, antes, é necessário conhecer a sua base e a sua altura.

Para saber a área do retângulo, basta calcular o produto entre a base e a altura da figura.
A = b · h
b → base
h → altura
Exemplo:
Um retângulo possui lados medindo 12 cm e 6 cm, então, qual é a sua área?
Resolução:
Sabemos que b = 12 e c = 6. Substituindo na fórmula, temos que:
A = b · h
A = 12 ·6
A = 72 cm2
O losango também possui 4 lados, porém todos congruentes. Para calcular a área do losango, é necessário conhecer o comprimento das suas diagonais, a diagonal maior e a diagonal menor.
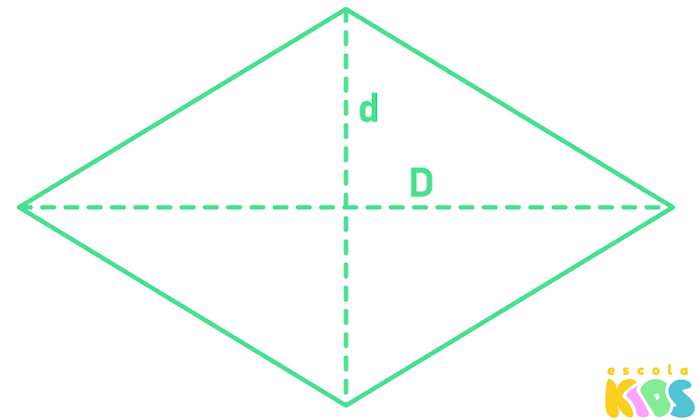
A área do losango é igual ao produto entre os comprimentos da diagonal maior e da diagonal menor dividido por 2.
![]()
D → comprimento da diagonal maior
d → comprimento da diagonal menor
Exemplo:
Um losango possui diagonal menor igual a 6 cm e diagonal maior igual a 11 cm, então a sua área é igual a:
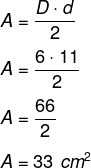
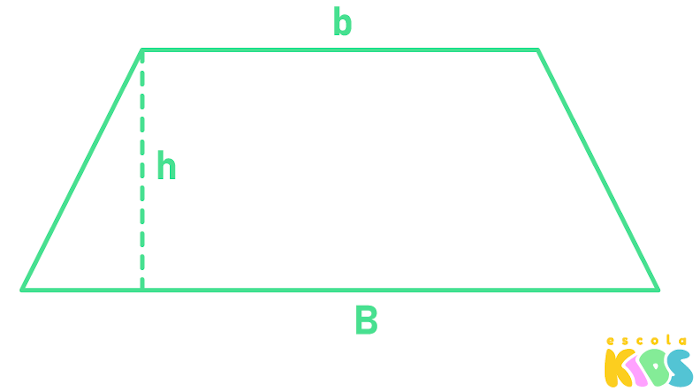
O último quadrilátero é o trapézio, ele possui dois lados paralelos, conhecidos como base maior e base menor, e dois lados não paralelos. Para calcular a área de um trapézio, é necessário conhecer o comprimento de cada base e o comprimento da sua altura.
![]()
B → base maior
b → base menor
h → altura
Exemplo:
Qual é a área do trapézio que possui base maior igual a 8 cm, base menor igual a 4 cm e 3 cm de altura?
Resolução:
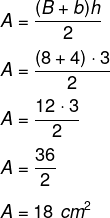
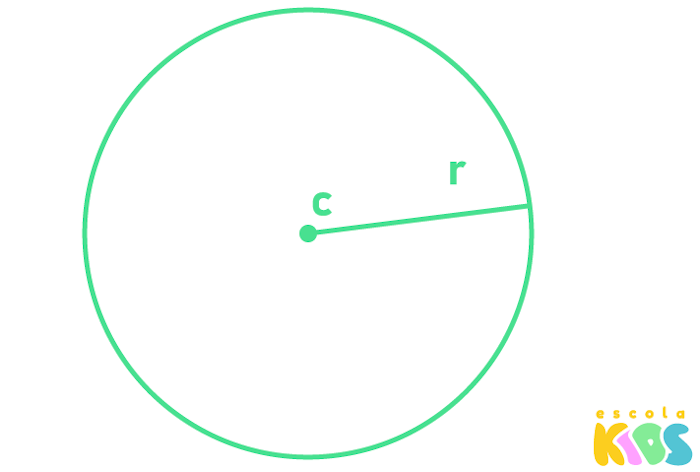
O círculo é formado pela região que está contida dentro de uma circunferência, que é o conjunto de pontos que estão a uma mesma distância do centro. O principal elemento do círculo para cálculo de área é o seu perímetro.
A = πr2
r → raio
O π é uma constante utilizada para cálculos envolvendo círculos. Como se trata de um número irracional, quando queremos a área do círculo, podemos utilizar uma aproximação para ele, ou então simplesmente utilizar o símbolo π.
Exemplo:
Calcule a área de um círculo de raio r = 5 cm (use π = 3,14).
Resolução:
Substituindo na fórmula, temos que:
A = πr2
A = 3,14 · 52
A = 3,14 · 25
A = 78,5 cm2
Leia também: Congruência de figuras geométricas — quais são os critérios?
Questão 1
(Enem) Uma empresa de telefonia celular possui duas antenas que serão substituídas por uma nova, mais potente. As áreas de cobertura das antenas que serão substituídas são círculos de raio
2 km, cujas circunferências se tangenciam no ponto O, como mostra a figura.
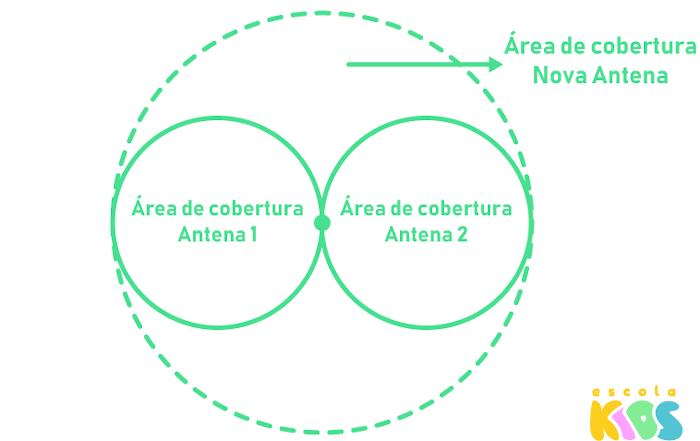
O ponto O indica a posição da nova antena, e sua região de cobertura será um círculo cuja circunferência tangenciará externamente as circunferências das áreas de cobertura menores.
Com a instalação da nova antena, a medida da área de cobertura, em quilômetros quadrados, foi ampliada em
A) 8π.
B) 12π.
C) 16π.
D) 32π.
E) 64π.
Resolução:
Alternativa A
Na imagem é possível identificar 3 círculos; os 2 menores possuem raio de 2 km, então, sabemos que:
A1 = πr2
A1 = π ⸳ 22
A1 = 4 π
Como há 2 círculos menores, então a área que eles ocupam juntos é 8 π.
Agora calcularemos a área do círculo maior, que possui raio de 4 km:
A2 = πr2
A2 = π⸳ 42
A2 = 16 π
Calculando a diferença entre as áreas, temos que 16π– 8π = 8 π.
Questão 2
Um losango possui diagonal menor (d) medido 6 cm e diagonal maior (D) medindo o dobro da diagonal maior menos 1, então, a área desse losango é igual a:
A) 33 cm2
B) 35 cm2
C) 38 cm2
D) 40 cm2
E) 42 cm2
Resolução:
Alternativa A
Sabendo que d = 6, então temos que D = 2 · 6 – 1 = 12 – 1 = 11 cm. Calculando a área, temos que: