O conjunto dos números irracionais é formado pelos números que não podem ser representados como frações. Em algumas situações, o conjunto dos números racionais não era suficiente para a resolução de problemas, foi quando se percebeu a existência dos números irracionais, como as raízes não exatas, as dízimas não periódicas, o π, entre outros.
Leia também: Qual o valor de um algarismo?
No decorrer da história, na aplicação do teorema de Pitágoras em um triângulo retângulo de lados medindo 1, percebeu-se que a resposta era igual à raiz do número 2.
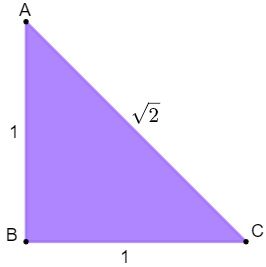
Acontece que essa resposta, aparentemente simples, tornou possível a descoberta de um novo conjunto numérico. Na tentativa de encontrar-se a resposta para essa raiz quadrada de 2, encontrou-se um número decimal conhecido como dízima não periódica, que é impossível de ser representada como uma fração. Isso fez necessária a criação de um novo conjunto, os irracionais, já que, até aquele momento, todos os números eram racionais (que podem escritos como fração).
|
O conjunto dos números irracionais é composto por todos os números que não podem ser escritos na forma de uma fração. |
Para que um número seja considerado irracional, ele precisa respeitar a definição, ou seja, ele não pode ser representado como uma fração. Esses números são as raízes não exatas, as dízimas não periódicas e alguns casos especiais, como a constante π (lê-se: pi) ou o número ɸ (lê-se: fi), entre outros.
Quando o número não é um quadrado perfeito, é conhecido como raiz não exata. Veja alguns exemplos:
![]()
Ao resolver-se essas raízes, a resposta sempre vai ser uma aproximação, o que chamamos de dízimas não periódicas.
![]()
Note que a parte decimal é infinita e que não existe um período, ou seja, uma sequência que faça com que a gente consiga prever o próximo número da parte decimal, e é por isso que chamamos esse número de dízima não periódica. Não só as dízimas geradas por raízes não exatas, mas qualquer dízima não periódica é um número irracional.
• Número π: é bastante comum para cálculos envolvendo curvas, como área e comprimento de circunferência ou volume de cilindros e cones, e é um dos mais conhecidos números irracionais. Pelo fato de ser irracional, utilizamos um símbolo para representá-lo, ainda assim, π é uma dízima não periódica, e seu valor é igual a 3,14159265358979323846… São conhecidas várias casas desse número, mas normalmente utilizamos uma aproximação, com o valor de 3,14.
• Número ɸ: é conhecido também como número de ouro e é estudado desde a Antiguidade, descrevendo vários fenômenos da natureza, como a reprodução de populações de coelhos. Há também relato do uso dessa proporção em obras artísticas. Ele também é um número irracional, e por isso é representado pelo símbolo ɸ, sendo seu valor de: 1,61803398875…
• Constante de Euler: é utilizada para fenômenos que envolvem matemática financeira, e nas áreas de biologia, astronomia, entre outras. Ela também é um número irracional e, por isso, é representada pelo símbolo e, sendo seu valor de: 2,718281828459045235360…
Veja também: Números primos – número natural que possui apenas dois divisores
Acontece que um número qualquer pode ser classificado como racional ou irracional. De forma direta, o número racional é todo número que pode ser escrito como fração. São números racionais os decimais exatos, as dízimas periódicas, os números inteiros. Já os números irracionais são o oposto disso, ou seja, são os que não podem ser escritos como fração, como citamos, são eles as dízimas não periódicas e raízes não exatas.
A dízima 3,12121212… é periódica, note que na sua parte decimal existe um período, que é o número 12, que sempre se repete, logo, esse número é racional.
A dízima 6,1249375…. é não periódica, note que não há um período na sua parte decimal, o que faz com que esse número seja irracional.

Questão 1 - Qual dos números a seguir pode ser classificado como irracional?

Resolução
Alternativa C.
a) Sabemos que 25 é um quadrado perfeito, ou seja, sua raiz quadrada é exatamente igual a 5, logo, esse é um número racional.
b) Ao calcular a raiz de 81, sabemos que seu resultado é 9, o que faz com que aquele número seja racional.
c) 10 não possui raiz quadrada exata, ou seja, ele é um número irracional, o que torna a alternativa C correta.
d) 5,1888 é um número decimal exato, logo, ele é racional.
e) 1,2323… é uma dízima com o período igual a 23, logo, trata-se de um número racional.
Questão 2 - Sobre os números irracionais, julgue as afirmativas seguintes como verdadeiras ou falsas:
I - Toda raiz quadrada é um número irracional.
II - Toda dízima não periódica é um número irracional.
III - O número ɸ e o número π são exemplos de números irracionais.
De acordo com o julgamento das sentenças, é correto afirmar que:
a) Somente a afirmativa I é verdadeira.
b) Somente a afirmativa II é verdadeira.
c) Somente as afirmativas II e III são verdadeiras.
d) Somente as afirmativas I e II são verdadeiras.
e) Todas as afirmativas são verdadeiras.
Resolução
Alternativa C.
I - Falsa, pois somente a raiz quadrada não exata é um número irracional.
II - Verdadeira. Dízimas não periódicas são números irracionais.
III - Verdadeira, pois os números ɸ e π são dízimas não periódicas, logo, são números irracionais.