A raiz quadrada é um tipo de operação matemática, assim como a adição, multiplicação, entre outras. Ela é a operação inversa da potência de dois, ou seja, calcular a raiz quadrada de um número a é procurar o número elevado a 2 que resulta em a.
Além disso, essa raiz pode ser exata ou não. Quando ela é exata, o número é chamado de quadrado perfeito. Na geometria, ela é útil para determinamos o lado de quadrados.
Leia também: Potenciação e radiciação de frações – como resolver?
Na raiz quadrada, o índice da raiz é 2. Ela é a mais comum entre as radiciações, mas também é possível calcular raiz cúbica, raiz quarta, entre outras raízes.
A radiciação é o inverso da potenciação. Por exemplo, se eu pedir a raiz quinta de um número n, estamos procurando qual é o número que, multiplicado por ele 5 vezes, resulta em n.
A operação é representada por:
![]()
![]() radical
radical
n→ índice
a→ radicando
b→ raiz
Como vamos fazer o estudo da raiz quadrada, o índice será sempre igual a 2. Em uma radiciação, quando o índice é 2, não precisamos escrevê-lo.
![]()
O cálculo da raiz quadrada pode ser feito de cabeça por meio de tabuada quando conhecemos a raiz. Quando o número é muito grande, uma alternativa é realizar a fatoração desse número. Calcular a raiz quadrada de a é encontrar o número b que, quando multiplicamos b .b, resulta em a.
Exemplos
Uma raiz quadrada pode ser exata ou não. Para que a gente consiga classificar, precisamos levar em consideração se a resposta é um número racional ou um número irracional.
Uma raiz quadrada é exata quando resulta em um número racional, como uma fração, um número inteiro, um número decimal, desde que, ao multiplicar esse número por ele mesmo, encontremos exatamente o radicando.
Exemplos
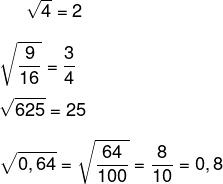
Quando o número para o qual desejamos calcular a raiz quadrada exata é muito grande, o ideal é recorrer à fatoração desse número. Como estamos calculando a raiz quadrada, vamos agrupar essa fatoração como potências de dois conforme o exemplo a seguir.
Exemplo
Calcule a raiz quadrada de 3600.

Agora que realizamos a fatoração, vamos calcular a raiz de 3600 na forma fatorada.
Podemos perceber que a raiz de um número ao quadrado é igual ao próprio número. Por exemplo, sabemos que 3 ao quadrado é 9 e que a raiz de 9 é igual ao próprio 3. Então podemos simplificar o expoente 2 com o radical.
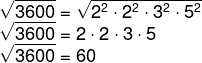
Na raiz exata, quando a resposta é um número natural, ele é conhecido como quadrado perfeito. Veja todos os quadrados perfeitos de 0 até 100.
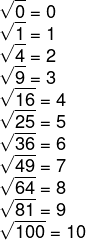
Os quadrados perfeitos de 0 até 100 são 0, 1, 4, 9, 16, 25, 36, 49, 64, 81 e 100.
Existem casos em que a raiz não é exata. Quando isso acontece, podemos encontrar a melhor aproximação possível para a raiz desse número, já que a resposta é um número irracional. Para essa aproximação, vamos utilizar os quadrados perfeitos que já conhecemos.
Exemplo
Para encontrar a raiz de 40, vamos compará-la com as raízes exatas que conhecemos. Analisando os quadrados perfeitos, sabemos que 40 está entre 36 e 49.
![]()
Agora vamos encontrar o número decimal entre 6 e 7 que está mais próximo de 40.
6,1² = 37,21
6,2²= 38,44
6,3²=39,69
6,4²=40,96 → passou de 40, então vamos usar o número decimal anterior para a aproximação.
![]()
Perceba que 6,3² não dá exatamente 40, mas chega próximo, por isso essa raiz quadrada não é exata.
Veja também: Cálculo de raízes – formas de resolver
Alguns livros de história da matemática dizem que a raiz quadrada surgiu para resolver problemas de áreas de quadrado. Suponha que queiramos achar o lado de um terreno que tem formato de um quadrado e que sua área seja igual a 169 m².

Como a área do quadrado é calculada por l², então calcular a raiz de 169, geometricamente, é encontrar o lado do quadrado que possui essa área.
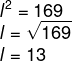
O lado do quadrado é de 13 metros.

Questão 1 - Qual é a melhor aproximação para a raiz quadrada de 72?
A) 8,1
B) 8,2
C) 8,3
D) 8,4
E) 8,5
Resolução
Alternativa D.
Sabemos que 72 está entre os quadrados perfeitos 64 e 81, então temos que:
![]()
8,1²= 65,61
8,2²= 67,24
8,3²= 68,89
8,4²= 70,56
8,5²= 72,25 → passou, então a melhor aproximação é a anterior, 8,4.
Questão 2 - Qual das raízes abaixo não é exata?

Resolução
Alternativa C.
a) Possui raiz exata igual a 11, pois 11² =121.
b) Possui raiz exata igual a 1,3, pois 1,3² = 1,69.
c) Não possui raiz exata
d) Possui raiz exata, pois o numerador 1²=1 e o denominador 2²=4, logo a raiz dessa fração é igual a ½.
e) Possui raiz exata igual a 1.