Potenciação

A potenciação é uma operação matemática que representa a multiplicação sucessiva de um número por ele mesmo. Ao multiplicar o 3 por ele mesmo 4 vezes, isso pode ser representado pela potência 3 elevada a 4: 3⁴.

 Essa operação possui propriedades importantes que facilitam o cálculo das potências. Assim como a multiplicação possui a divisão como operação inversa, a potenciação possui a radiciação como operação inversa.

Cada elemento da potenciação recebe um nome específico:

aⁿ = b

a → base

n→ expoente

b→ potência

Leia também: Potenciação e radiciação de frações

Como ler uma potência?

Saber ler uma potência é uma tarefa importante. A leitura é sempre feita começando pelo número que está na base elevado ao número que está no expoente, como nos exemplos a seguir:

Exemplos:

a) 4³ → Quatro elevado a três, ou quatro elevado à terceira potência, ou quatro elevado ao cubo.

b) 3⁴ → Três elevado a quatro, ou três elevado à quarta potência.

c) (-2)¹ → Menos dois elevado a um, ou menos dois elevado à primeira potência.

d) 8² → Oito elevado a dois, ou oito elevado à segunda potência, ou oito elevado ao quadrado.

As potências de expoente 2 podem ser chamadas também de potências elevadas ao quadrado, e as potências de grau 3 podem ser chamadas de potências elevadas ao cubo, como nos exemplos anteriores.

Cálculo de potências

Para encontrar o valor de uma potência, precisamos realizar as multiplicações como nos exemplos a seguir:

a) 3²= 3 · 3 = 9

b) 5³= 5·5·5 = 125

c) 10⁶ = 10 · 10 · 10 · 10 · 10 · 10 = 1 000 000

Tipos de potência

Existem alguns tipos específicos de potência.

1º caso – Quando a base for diferente de zero, podemos afirmar que todo número elevado a zero é igual a 1.

Exemplos:

a) 10⁰=1

b) 1293⁰=1

c) (-32)⁰=1

d) 8⁰=1

2º caso - Todo número elevado a 1 é ele mesmo.

Exemplos:

a) 9¹ = 9

b) 12¹ = 12

c) (-213)¹= - 213

d) 0¹ = 0

3º caso - 1 elevado a qualquer potência é igual a 1.

Exemplos:

a) 1²¹ = 1

b) 1³ = 1

c) 1⁵⁰⁰=1

4º caso - Base de uma potenciação negativa

Quando a base é negativa, separamos em dois casos: quando o expoente for ímpar, a potência será negativa; quando o expoente for par, a resposta será positiva.

Exemplos:

a) (-2)³ = (-2) · (-2) · (-2) = - 8 → Note que o expoente 3 é ímpar, logo a potência é negativa.

b) (-2)⁴= (-2) · (-2) · (-2) · (-2) = 16 → Note que o expoente 4 é par, por isso a potência é positiva.

Leia também: Potências com expoente negativo

Potência com expoente negativo

Para calcular a potência com expoente negativo, escrevemos o inverso da base e trocamos o sinal do expoente.

Propriedades da potenciação

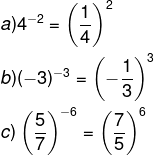
Além dos tipos de potenciação mostrados, a potenciação possui propriedades importantes para facilitar o cálculo de potência.

→ 1ª propriedade – Multiplicação de potências de mesma base

Ao realizarmos uma multiplicação de potências de mesma base, conservamos a base e somamos os expoentes.

Exemplos:

a) 2⁴· 2³ = 2⁴⁺³=2⁷

b) 5³ · 5⁵ · 5²= 5³⁺⁵⁺² = 5¹⁰

→ 2ª propriedade – Divisão de potências de mesmo base

Quando encontramos uma divisão de potência de mesma base, conservamos a base e subtraímos os expoentes.

Exemplos:

a) 3⁷ : 3⁵ = 3^7-5 = 3²

b) 2³ : 2⁶ = 2^3-6 = 2^-3

→ 3ª propriedade – Potência de potência

Ao calcular a potência de uma potência, podemos conservar a base e multiplicar os expoentes.

Exemplos:

a) (5²)³ = 5^2·3 = 5⁶

b) (3⁵)⁴ = 3^5·4 = 3 ²⁰

→ 4ª propriedade – Potência de um produto

Quando há uma multiplicação de dois números elevada a um expoente, podemos elevar cada um desses números ao expoente.

Exemplos:

a)(5 · 7)³ = 5³ · 7³

b)( 6·12)⁸ = 6⁸ · 12⁸

→ 5ª propriedade – Potência do quociente

Para calcular potências de um quociente ou até mesmo de uma fração, o modo de realizar é muito parecido com a quarta propriedade. Se há uma divisão elevada a um expoente, podemos calcular a potência do dividendo e do divisor separadamente.

a) (8:5)³ = 8³ : 5³

Potenciação e radiciação

A radiciação é a operação inversa da potenciação, ou seja, ela desfaz o que foi feito pela potência. Por exemplo, ao calcularmos a raiz quadrada de 9, estamos procurando o número elevado ao quadrado que resulta em 3. Então, para entender uma delas, é fundamental que se domine a outra. Em equações, também é bastante comum o uso da radiciação para eliminar uma potência de uma incógnita, e também o contrário, ou seja, usarmos potenciação para eliminar a raiz quadrada de uma incógnita.

Exemplo

- Calcule o valor de x, sabendo que x³ = 8.

Para calcular o valor de x, é necessário realizar a operação inversa da potenciação, ou seja, a radiciação. Na realidade, estamos buscando qual é o número que, ao ser elevado ao cubo, tem como resultado o número 8.

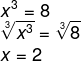
Essa relação entre a radiciação e a potenciação torna fundamental dominar as regras de potenciação para avançar o aprendizado sobre a radiciação.

Leia também: Como calcular raízes usando potências?

Exercícios resolvidos sobre potenciação

1) (PUC-RIO) O maior número abaixo é:

a) 3³¹

b)8¹⁰

c)16⁸

d)81⁶

e)243⁴

Resolução:

Realizar a comparação calculando cada um deles seria uma tarefa difícil, então vamos simplificar as alternativas,

a) 3³¹ → já está simplificada

b) 8 = 2³ → (2³)¹⁰ = 2³⁰

c) 16 = 2⁴ → (2⁴)⁸ = 2³²

d) 81 = 3⁴ → (3⁴)⁶ = 3²⁴

e) 243=3⁵ → (3⁵)⁴ = 3²⁰

Logo, a maior das potências é a letra A.

2) A simplificação da expressão [3¹⁰: (3⁵. 3)²]^- é igual a:

a)3^-4

b)3⁴

c)3⁰

d)3²

e)3^-2

Resolução:

[3¹⁰: (3⁵. 3)²]^-2

[3¹⁰: (3⁶)²]^-2

[3¹⁰: 3¹²]^-2

[3^-2]^-2

3⁴

Letra B.