As frações são uma forma de representar a divisão entre dois números. O número de cima da fração é chamado de numerador e o número de baixo é conhecido como denominador.

A fração é uma forma de representar uma divisão em partes iguais. Ela indica quantas partes de um todo estão sendo consideradas. O número que está localizado na parte superior da fração é chamado de numerador e representa a quantidade de partes que estão sendo tomadas. Já o número que está na parte inferior é chamado de denominador e indica em quantas partes iguais o todo foi dividido.
Leia também: Dicas e exemplos de como fazer uma divisão

A fração é uma forma de expressar a divisão entre dois números. De modo geral, escrever uma fração é escrever um número sobre outro: o numerador sobre o denominador.
Para fazer a leitura correta da fração, observamos o seu numerador e o seu denominador.
Exemplos:
Quando o numerador da fração é maior que 10, o padrão de leitura muda um pouco: o numerador continua sendo lido como número cardinal, e o denominador é lido como número cardinal seguido da palavra “avos”.
Exemplo:
As frações podem ser próprias, impróprias ou aparentes.
Na fração própria, o numerador é menor que o denominador.
Exemplos:
A fração é imprópria se o numerador for maior que o denominador.
Exemplo:
A fração é aparente quando ela representa um número inteiro.
Exemplos:
Frações equivalentes são frações que, apesar de terem numeradores e denominadores diferentes, representam a mesma quantidade ou a mesma parte de um todo, ou seja, elas têm o mesmo valor, embora os números que as formam sejam diferentes.
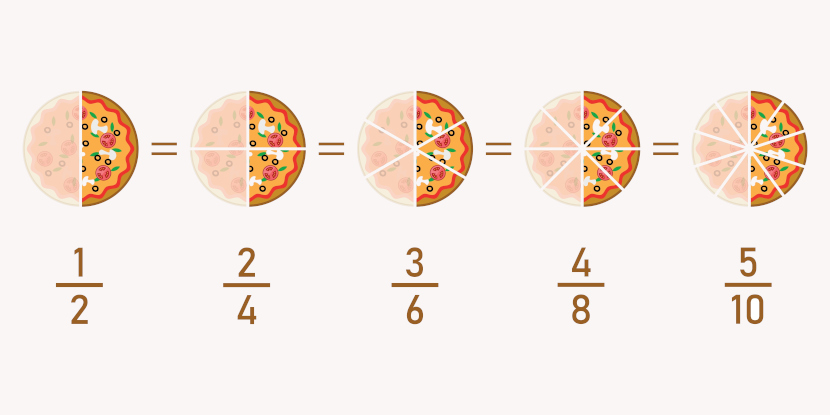
A forma irredutível de uma fração é quando ela está escrita na forma mais simples possível, ou seja, quando não é mais possível simplificá-la. Isso acontece quando o numerador e o denominador) não têm nenhum divisor comum além do número 1.
→ Exemplo 1
A fração \(\frac{6}{8} \) não está na sua forma irredutível, pois podemos dividir seu numerador e o seu denominador por 2 para simplificá-la.
6 : 2 = 3
8 : 2 = 4
A fração \(\frac{3}{4} \) é a forma irredutível da fração \(\frac{6}{8} \), pois são equivalentes e a fração \(\frac{3}{4} \) não pode ser simplificada.
→ Exemplo 2
Encontraremos a fração irredutível da fração \(\frac{15}{12}\).
Resolução:
Para encontrar a fração irredutível, vamos simplificá-la dividindo o numerador e o denominador por um mesmo número. Nesse caso, podemos dividir por 3:
\(\frac{15^{\div3}}{12_{\div3}} = \frac{5}{4} \)
Para transformar a fração em um número decimal, realizamos a divisão do numerador pelo numerador.
Exemplo:
\(\frac{7}{2} \)
Calcularemos a divisão de 7 por 2:
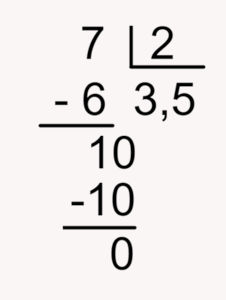
Então, temos que:
\(\frac{7}{2} = 3{,}5\)
Para transformar um número decimal em fração, é necessário seguir os seguintes passos:
→ Exemplo 1
Transformando 0,5 em fração:
\(0{,}5 = \frac{5}{10} \)
Simplificando:
\(\frac{5^{\div5}}{10_{\div5}} = \frac{1}{2} \)
→ Exemplo 2
Transformando 0,75 em fração:
\(0{,}75 = \frac{75}{100} \)
Simplificando:
\(\frac{75^{\div25}}{100_{\div25}} = \frac{3}{4} \)
→ Exemplo 3:
Transformando 1,2 em fração:
\(1{,}2 = \frac{12}{10} \)
Simplificando:
\(\frac{12^{\div2}}{10_{\div2}} = \frac{6}{5} \)
Podemos realizar as quatro operações entre frações, ou seja, adição, subtração, multiplicação e divisão.
Quando o denominador é o mesmo, somamos o numerador e conservamos o denominador.
Exemplo:
\(\frac{2}{7} + \frac{3}{7} = \frac{5}{7} \)
Primeiro, é necessário igualar os denominadores, encontrando o mínimo múltiplo comum (MMC). Depois, faz-se a soma dos numeradores.
Exemplo:
\(\frac{1}{4} + \frac{1}{6} = \frac{3}{12} + \frac{2}{12} = \frac{5}{12}\)
Segue o mesmo processo da adição.
Mantém-se o denominador e subtraem-se os numeradores.
Exemplo:
\(\frac{4}{5} - \frac{3}{5} = \frac{1}{5}\)
Primeiro, é necessário igualar os denominadores, encontrando o mínimo múltiplo comum (MMC). Depois, faz-se a subtração dos numeradores.
Exemplo:
\(\frac{2}{4} - \frac{1}{5} = \frac{10}{20} - \frac{4}{20} = \frac{6}{20}\)
Multiplicam-se diretamente os numeradores e os denominadores.
Exemplo:
\(\frac{3}{4} \times \frac{5}{7} = \frac{15}{28} \)
Multiplica-se a primeira fração pelo inverso da segunda:
Exemplo:
\(\frac{3}{4} : \frac{2}{5} = \frac{3}{4} \times \frac{5}{2} = \frac{15}{8} \)
Leia também: Como calcular números em porcentagem
Amanda está fazendo uma receita de bolo e usou 3/4 de xícara de açúcar no preparo da massa e mais 1/2 de xícara no preparo da cobertura. Quantas xícaras de açúcar ela usou no total?
A) 1 xícara
B) 1 e 1/4 xícara
C) 1 e 1/2 xícara
D) 1 e 2/3 xícaras
E) 2 xícaras
Resolução:
Alternativa B.
Calculando a soma, temos que:
\(\frac{3}{4} + \frac{1}{2} = \frac{3}{4} + \frac{2}{4} = \frac{5}{4} \)
Sabemos que \(\frac{5}{4} = \frac{4}{4} + \frac{1}{4} = 1 + \frac{1}{4} \). Então foi utilizada 1 xícara mais 1/4.
Questão 2
Joana comprou 2/5 de um metro de tecido e usou 3/4 desse pedaço para fazer uma almofada. Quantos metros de tecido foram usados na almofada?
A) 3/20
B) 3/10
C) 1/2
D) 6/9
E) 8/15
Resolução:
Alternativa B.
Calculando o produto, temos que:
\(\frac{2}{5} \times \frac{3}{4} = \frac{6}{20} \)
Simplificando:
\(\frac{6^{\div2}}{20_{\div2}} = \frac{3}{10} \)
Fontes
GIOVANNI, José Ruy; GIOVANNI JÚNIOR, José Ruy; CASTRUCCI, Benedicto. A conquista da matemática: 8º ano. 1. ed. São Paulo: FTD Educação, 2022.
DANTE, Luiz Roberto. Matemática: contexto & aplicações: volume 2. 1. ed. São Paulo: Ática, 2019.