Você já deve ter-se deparado com uma situação do cotidiano em que se utiliza porcentagem, seja em descontos para comprar um determinado produto, seja em multas devido a atrasos de conta. Porcentagem nada mais é que uma razão que possui o 100 como denominador.
Utilizamos o símbolo % para representar a porcentagem, 20%, por exemplo, significa que temos 20 partes de algo que foi divido em 100. Podemos usar também a representação decimal (ou fracionária) para representar uma porcentagem. A representação decimal ou fracionária é de grande importância e utilizamo-la para o cálculo da porcentagem de um número.
Leia também: Proporção – igualdade entre duas ou mais razões
A porcentagem é empregada o tempo todo nas relações comerciais e em várias outras situações do dia a dia. É bastante comum ver, em vitrines de lojas ou em contas de energia, por exemplo, o uso do símbolo de porcentagem para passar alguma informação. Chamamos de porcentagem qualquer razão que tenha como denominador o número 100, e utilizamo-la para comparar a partes de um todo, por exemplo, se eu digo 30%, isso significa que tenho 30 partes de algo que foi divido em 100 partes.
Para representar a porcentagem de um número, é bastante comum escrevermos ele seguido do símbolo %, ou seja, a representação 5%, por exemplo, é lida como cinco por cento. Considerando-se essa representação pelo símbolo da porcentagem, existem três formas de representar-se a porcentagem: a percentual, a fracionária e a decimal.
É a representação que utiliza o símbolo %, como nos exemplos a seguir:
→ 20% (lê-se: vinte por cento)
→ 5% (lê-se: cinco por cento)
→ 13,25% (lê-se: treze vírgula vinte e cinco por cento)
Outra representação bastante comum é a fracionária, utilizada para cálculos envolvendo porcentagem. Basta escrever uma fração do número sobre 100.
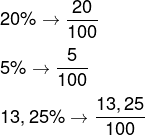
Também pode ser utilizada para realização de cálculos, como vimos, 20% significa a divisão de 20 por 100, então, para representar-se essa porcentagem na forma decimal, basta a divisão:
20% = 20 : 100 = 0,20 = 0,2
5% = 5 : 100 = 0,05
13,25% = 13,25 : 100 = 0,1325
Veja também: Simplificação de frações: o que é e como fazer?
Existem várias aplicações da porcentagem, e para cada uma delas há métodos diferentes de resolução. Para resolver-se problemas de porcentagem, é bastante comum o uso da regra de três simples ou de operações com frações e números decimais.
Exemplo 1:
Calcule 20% de 400.
Método 1: Para isso, podemos realizar a representação fracionária de 20% e, posteriormente, multiplicar essa fração por 400:
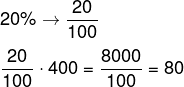
Método 2: Caso queira, em vez de representar 20% como uma fração, podemos utilizar a representação decimal, ficando assim:
20% → 0,2
0,2 · 400 = 80
O que significa que 80 corresponde a 20% de 400.
Exemplo 2:
25 corresponde a quantos por cento de 750?
Nesse caso é bastante comum o uso da regra de três ou até mesmo a simples divisão.
Método 1: Regra de três simples
|
Valor |
Porcentagem |
|
750 |
100% |
|
90 |
x |
Multiplicando cruzado, temos que:
750x = 90 · 100
750x = 9 000
x = 9 000 : 750
x = 12
Método 2: Divisão
Basta realizar a divisão de 90 por 750, para encontrarmos a representação decimal da porcentagem.
90 : 740 = 0,12 → 12%
Isso significa que 90 corresponde a 12% de 750.
Acesse também: Dízima periódica – número que possui a sua parte decimal infinita e periódica
Questão 1 – (Enem 2014) Uma ponte precisa ser dimensionada de forma que possa ter três pontos de sustentação. Sabe-se que a carga máxima suportada pela ponte será de 12 t. O ponto de sustentação central receberá 60% da carga da ponte, e o restante da carga será distribuído igualmente entre os outros dois pontos de sustentação. No caso de carga máxima, as cargas recebidas pelos três pontos de sustentação serão, respectivamente:
A) 1,8 t; 8,4 t; 1,8 t.
B) 3,0 t; 6,0 t; 3,0 t.
C) 2,4 t; 7,2 t; 2,4 t.
D) 3,6 t; 4,8 t; 3,6 t.
E) 4,2 t; 3,6 t; 4,2 t.
Resolução
Alternativa C
Queremos encontrar 60% de 12t, que é a carga recebida pelo ponto de sustentação central.
0,6 · 12 = 7,2 t. Sendo assim, o ponto central receberá 7,2 toneladas, e o restante será dividido igualmente entre os outros pontos de sustentação.
12 – 7,2 = 4,8
Como há dois pontos 4,8 : 2 = 2,4, os três pontos receberão, respectivamente: 2,4 t; 7,2 t; e 2,4 t.
Questão 2 – Laura recebeu de herança R$ 24 000,00. Parte do dinheiro ela gastou com as dívidas que ela tinha, e aproveitou também para comprar alguns eletrodomésticos para o seu apartamento. Com os R$ 10 000,00 restantes, ela emprestou R$ 6 000,00 para sua amiga e guardou o resto. Em relação a essa situação: da herança, qual foi a porcentagem que Laura emprestou para a sua amiga?
A) 25%
B) 30%
C) 15%
D) 45%
E) 18%
Resolução
Alternativa A
Para calcular-se a porcentagem, basta a divisão de 6 000 por 22 000. Sendo assim, temos que:
6 000 : 24 000 = 0,25 → 25%