A dízima periódica é um número que possui sua parte decimal infinita e periódica, isto é, em sua parte decimal, há um número que se repete infinitamente. Considerada um número racional, ela pode ser representada como uma fração, que é chamada de fração geratriz. Também pode ser simples ou composta.
Leia também: Divisão de frações
Além da forma de fração, conhecida como fração geratriz, a dízima periódica pode ser representada como um número decimal de duas maneiras. Podemos inserir, ao final do número, reticências ( … ) ou podemos colocar um traço acima do seu período (parte que se repete na dízima), logo uma mesma dízima pode ser representada de dois jeitos. Exemplos:
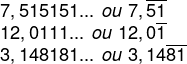

Uma dízima periódica simples possui uma parte inteira (que vem antes da vírgula) e o período, que vem depois da vírgula.
Exemplos:
1,333…
1→ parte inteira
3 → período
0,76767676…
0 → parte inteira
76 → período
Uma dízima periódica composta possui parte inteira (que vem antes da vírgula), parte não periódica e período, que vem depois da vírgula. O que diferencia uma dízima periódica simples de uma composta é que, na simples, só há o período depois da vírgula; na composta, existe uma parte que não se repete depois da vírgula.
Exemplos:
1,5888…
1 → parte inteira
5 → parte não periódica
8→ período
32,01656565…
32 → parte inteira
01 → parte não periódica
65 → período
Leia também: Números decimais – aprenda a realizar operações matemáticas com esses números
Encontrar a fração que gera a dízima nem sempre é uma tarefa fácil. Precisamos dividir em dois casos: quando a dízima é simples e quando ela é composta. Para encontrar a fração geratriz, utilizamos uma equação.
Exemplo:
- Vamos encontrar a fração geratriz da dízima 1,353535…
Seja x = 1,353535…, como essa dízima possui 2 números no seu período (35), vamos multiplicar x por 100. Então,
100x = 135,3535…
Agora realizando a subtração,
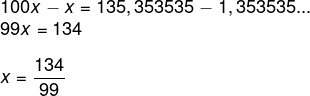
Existe um método prático para encontrarmos a fração geratriz de uma dízima periódica simples que evita a construção de equações. Vamos encontrar novamente a fração geratriz da dízima 1,353535…, porém pelo método prático.
1º passo: identificar período e parte inteira.
Parte inteira → 1
Período → 35
2º passo: encontrar o numerador.
O numerador é o número formado pela parte inteira e o período (no exemplo, é 135) menos a parte inteira, ou seja:
135 – 1 = 134
3º passo: encontrar o denominador.
Para isso, vamos avaliar quantos números têm no período da dízima, e, para cada número, acrescentaremos o número 9 no denominador. Como nesse caso há dois números, o denominador é 99. Logo, a fração geratriz é:
![]()
Um pouco mais complicada de se encontrar, a fração geratriz de uma dízima periódica composta pode ser determinada também por meio de uma equação.
Exemplo:
- Vamos encontrar a fração geratriz da dízima 2,13444...
Seja x = 2,13444…. vamos multiplicar por 100 para que, após a vírgula, fique somente a parte periódica. Então,
100x = 213,444….
Por outro lado, sabemos que 1000x= 2134,444….
Agora faremos a subtração:
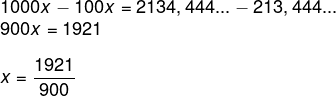
Para a dízima periódica composta, também existe um método prático, que vamos usar para encontrar a fração geratriz da dízima periódica composta 2,13444…
1º passo: identificar as partes da dízima periódica.
Parte inteira→ 2
Parte não periódica → 13
Período →4
2º passo: encontrar o numerador.
Para calcular o numerador, vamos escrever o número formado pela parte inteira, parte não periódica e período, ou seja, 2134 menos a parte inteira e a parte não periódica, ou seja, 213.
2134 – 213 = 1921
3º passo: encontrar o denominador.
No denominador, para cada número no período, acrescentamos um 9 e, para cada número na parte não periódica, um 0. No exemplo, o denominador é 900.
A fração geratriz é:
![]()
Leia também: Divisão com vírgula – como fazer?
1) Dos números a seguir, assinale aquele que corresponde a uma dízima periódica composta.
a) 3,14159284…
b) 2,21111
c) 0,3333….
d) 1,21111….
Resolução:
Alternativa D.
Analisando as alternativas, temos que:
a) É uma dízima não periódica. Perceba que, por mais que seja infinita, não há como prever os próximos números.
b) Não é uma dízima.
c) É uma dízima periódica simples.
d) Verdadeira, pois é uma dízima periódica composta.
2) A fração geratriz da dízima 12,3727272… é ?
a) 1372/9999
b) 12249/990
c) 12/999
d) 123/990
Resolução:
Pelo método prático, temos que: 12372 – 123= 12249, que será o numerador.
Analisando a parte decimal:
3 → parte não periódica
72 → período
990 → denominador
A fração que melhor representa é 12249/990, letra B.