Equação do 1º grau

Na Matemática, a equação é uma igualdade que envolve uma ou mais incógnitas. Quem determina o “grau” dessa equação é o expoente dessa incógnita, ou seja, se o expoente for 1, temos a equação do 1º grau. Se o expoente for 2, a equação será do 2º grau; se o expoente for 3, a equação será de 3º grau.

Para exemplificar:

4x + 2 = 16 (equação do 1º grau)

x² + 2x + 4 = 0 (equação do 2º grau)

x³ + 2x² + 5x – 2 = 0 (equação do 3º grau)

A equação do 1º grau é apresentada da seguinte forma:

ax + b = 0

É importante dizer que a e b representam qualquer número real e a é diferente de zero (a 0). A incógnita x pode ser representada por qualquer letra, contudo, usualmente, utilizamos x ou y como valor a ser encontrado para o resultado final da equação. O primeiro membro da equação são os números do lado esquerdo da igualdade, e o segundo membro, o que estão do lado direito da igualdade.

Veja também: Método prático para resolver equações

Como resolver uma equação do primeiro grau

Para resolvermos umaa equação do primeiro grau, devemos achar o valor da incógnita (que vamos chamar de x) e, para que isso seja possível, é só isolar o valor do x na igualdade, ou seja, o x deve ficar sozinho em um dos membros da equação.

O próximo passo é analisar qual operação está sendo feita no mesmo membro em que se encontra x e “jogar” para o outro lado da igualdade fazendo a operação oposta e isolando x.

Primeiro exemplo:

x + 4 = 12

Nesse caso, o número que aparece do mesmo lado de x é o 4 e ele está somando. Para isolar a incógnita, ele vai para o outro lado da igualdade fazendo a operação inversa (subtração):

x = 12 – 4

x = 8

Segundo exemplo:

x – 12 = 20

O número que está do mesmo lado de x é o 12 e ele está subtraindo. Nesse exemplo, ele vai para o outro lado da igualdade com a operação inversa, que é a soma:

x = 20 + 12

x = 32

Terceiro exemplo:

4x + 2 = 10

Vamos analisar os números que estão no mesmo lado da incógnita, o 4 e o 2. O número 2 está somando e vai para o outro lado da igualdade subtraindo e o número 4, que está multiplicando, passa para o outro lado dividindo.

4x = 10 – 2

x = 10 – 2
      4

x =  8
      4

x = 2

Quarto exemplo:

-3x = -9

Esse exemplo envolve números negativos e, antes de passar o número para o outro lado, devemos sempre deixar o lado da incógnita positivo, por isso vamos multiplicar toda a equação por -1.

-3x = -9 .(-1)

3x = 9

Passando o número 3, que está multiplicando x, para o outro lado, teremos:

x =  9

      3

x = 3 

Quinto exemplo:

 2x  +  4  =  7
 3       5      8

Nesse caso, devemos fazer o MMC dos denominadores para que eles sejam igualados e, posteriormente, cancelados (sempre na intenção de isolar a incógnita x):

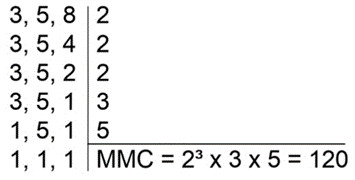
O próximo passo é igualar os denominadores com o resultado do MMC. Os numeradores são encontrados pela divisão do MMC pelo denominador e a multiplicação pelo numerador:

 (120 ÷ 3.2x)  +  (120 ÷ 5.4)  =  (120 ÷ 8.7)
    120                  120                   120  

 80x  +  96  =  105
   120     120     120  

Depois de igualados os denominadores, ele podem ser cancelados, restando a equação:

80x + 96 = 105

O 96 está somando e vai para o outro lado da igualdade subtraindo:

80x = 105 – 96

80x = 9

Para finalizar, o 80 que está multiplicando x vai para o outro lado da igualdade dividindo:

x =  9  
       80  

x = 0,1125

Obs.: Sempre que a incógnita x estiver entre parênteses e houver algum número de fora que esteja multiplicando esses parênteses, devemos distribuir a multiplicação do número para todos os componentes que estiverem dentro dos parênteses (esse processo é chamado de propriedade distributiva). Por exemplo:

5(3x – 9 + 5) = 0

Nesse caso, o 5 deve multiplicar todos os componentes de dentro dos parênteses para depois isolar a incógnita x:

15x – 45 + 25 = 0

15x – 20 = 0

15x = 20

x =  20   
     15  

                         x =  4  ou  x = 1,33333...    
3  

Saiba também: Equações que possuem expoente 2 na incógnita

Propriedade fundamental das equações

A propriedade fundamental das equações é também chamada de regra da balança. Não é muito utilizada no Brasil, mas tem a vantagem de ser uma única regra. A ideia é que tudo que for feito no primeiro membro da equação deve também ser feito no segundo membro com o objetivo de isolar a incógnita para se obter o resultado final. Veja a demonstração nesse exemplo:

3x + 12 = 27

Começaremos com a eliminação do número 12. Como ele está somando, vamos subtrair o número 12 nos dois membros da equação:

3x + 12 – 12 = 27 – 12

3x = 15

Para finalizar, o número 3 que está multiplicando a incógnita será dividido por 3 nos dois membros da equação:

 3x  =  15
 3        3

x = 5

Exercícios resolvidos

Exercício 1

Resolva as seguintes equações:

A. x + 4 = 15

Resolução:

x = 15 – 4

x = 11

B. 2x – 5 = x + 10

Resolução:

2x – x = 10 + 5

x = 15

C. 5x – 3x – 8 = – 29 + 9x

Resolução:

2x – 9x = – 29 + 8

– 7x = – 21 .( –1) Multiplicar todos por -1

7x = 21

x =  21
        7

x = 3

Exercício 2

Encontre o valor da incógnita na equação a seguir:

5 – (4x + 2) = 8 + 2(x – 1)

5 – 4x – 2 = 8 + 2x – 2

– 4x + 3 = 6 + 2x

– 4x – 2x = 6 – 3

– 6x = 3 .( –1)

6x = – 3

                             x = –  3 ÷ 3   (SIMPLIFICADO)
        6   3

x  = –  1 
          2