Clique para ver como as potências relacionam-se com uma técnica para cálculo de raízes que se baseia na decomposição do radicando em fatores primos!

O cálculo de raízes está profundamente ligado à multiplicação, mais especificamente à multiplicação em que os termos multiplicados são todos iguais. Quando isso acontece, costuma-se dizer que um número foi multiplicado por ele mesmo.
Os números multiplicados por eles mesmos são chamados de potências. É uma potência, portanto, qualquer número que for multiplicado por ele mesmo uma determinada quantidade de vezes. Esse número de vezes pode ser de 0 a infinito, dependendo do problema em questão e do tipo de estudo a ser realizado. Observe alguns exemplos de potências:
1·1·1 = 1
2·2·2 = 8
3·3 = 9
Como havia alguns casos em que essas potências eram multiplicações muito extensas, criou-se uma forma diferente de representar as potências. Por exemplo:
13 = 1·1·1 = 1
23 = 2·2·2 = 8
32 = 9
Portanto, para se representar a multiplicação do número 2 por ele mesmo seis vezes, podemos escrever, no lugar de 2·2·2·2·2·2, apenas 26. Essa operação é conhecida como potenciação. No exemplo seguinte,
an = b
a recebe o nome de base, n é o expoente e b é a potência (às vezes também chamamos an de potência). Dessa forma, potenciação é um tipo de multiplicação em que, dada uma base e um expoente, procura-se por uma potência, multiplicando-se essa base por ela mesma.
Muitas vezes, contudo, deparamo-nos com a situação inversa, em que é necessário encontrar a base que gerou uma potência. Esse processo é conhecido como radiciação (calcular a raiz). Utilizando o exemplo anterior, é apresentado o número b, então, devemos procurar pelo número a que foi multiplicado por ele mesmo n vezes. Esse cálculo é representado pelo seguinte símbolo:

Na imagem acima, procuramos a raiz enésima de b. Isso significa que buscamos um número a que, multiplicado por ele mesmo n vezes, tenha como resultado b. Na imagem acima, a é chamado de raiz enésima, b é chamado de radicando e n é chamado de índice.
Exemplo 1: Calcule a seguinte raiz:

Procuramos por um número que, multiplicado por ele mesmo 3 vezes, tenha 27 como resultado. Observe que não procuramos um número que, multiplicado por 3, é igual a 27, mas, sim, um número que multiplicado por si 3 vezes é 27. Portanto, procuramos pelo número A, que cumpre:
A·A·A = 27
Tentando realizar a multiplicação acima com o número 3 no lugar de A, obtemos:
3·3·3 = 27
Então,

Observe que 27 é resultado da multiplicação 3·3·3, que pode ser escrito como 33. Substituímos 27 por 33 e escrevemos a seguinte expressão:
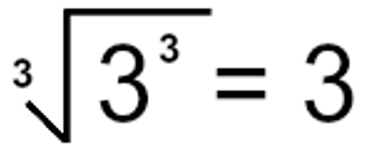
Essa observação leva ao entendimento de que é possível tentar escrever o radicando utilizando a sua decomposição em fatores primos.
Exemplo 2: Calcule a raiz quadrada de 576.

Observe, primeiramente, a decomposição de 576 em fatores primos:
576 |2
288 |2
144 |2
72 |2
36 |2
18 |2
9 |3
3 |3
1 |22·22·22·32
Observe que o resultado foi agrupado dois a dois. Isso acontece porque estamos calculando a raiz quadrada. Se fosse raiz cúbica, agruparíamos três a três; raiz quarta, quatro a quatro etc.
Agora basta calcular a raiz:
![]()
Por Luiz Paulo Moreira
Graduado em Matemática