A decomposição em fatores primos é uma ferramenta muito importante no desenvolvimento matemático, pois, com ela, é possível simplificar expressões numéricas ou algébricas e calcular MDC ou MMC de números inteiros.
A decomposição em fatores primos é um dos resultados mais importantes dentro do campo da álgebra e é conhecida formalmente como Teorema Fundamental da Aritmética, que afirma que todo número inteiro positivo maior que 1 pode ser escrito (ou decomposto) na forma de multiplicação de números primos.
Leia também: Propriedades da multiplicação para cálculo mental
É primordial entender o conceito de número primo, uma vez que vamos utilizá-los para decompor os números inteiros. Vamos aqui fazer uma breve retomada da definição de números primos.
|
Os números primos são aqueles que apresentam em sua lista de divisores somente o número 1 e eles mesmos. Para verificarmos se os números 11 e 21 são ou não primos, por exemplo, devemos listar os divisores de ambos os números: D (11) = {1, 11} D (21) = {1, 3, 7, 21} Veja que, ao listar os divisores de 11, aparecem somente o número 1 e ele mesmo, assim o número 11 é primo, o que não se aplica ao número 21, que apresenta mais números além de 1 e 21, portanto o número 21 não é primo. Os principais números primos que utilizamos para realizar a decomposição são os primeiros, assim, é muito importante que saibamos pelo menos os seguintes primos: P = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …} |
A decomposição em fatores primos é uma ferramenta muito poderosa dentro da matemática, uma vez que possibilita a simplificação de expressões algébricas e numéricas. Formalmente, a decomposição em fatores primos é conhecida como Teorema Fundamental da Aritmética, que afirma:
“Todo número inteiro maior que 1 pode ser escrito como sendo uma multiplicação de números primos.”
Além disso, essa decomposição é única para cada número, ou seja, ao decompor o número 12, por exemplo, ele será o único com tal fatoração. O número que admite uma decomposição é chamado de composto.
Para decompor um número composto, devemos realizar divisões sucessivas por números primos – isso se a divisão for possível – até que o quociente seja igual a 1. No final, devemos escrever os números primos utilizados em forma de multiplicação (forma fatorada). Veja os exemplos a seguir:
Escreva o número 24 na forma fatorada.
Para escrever o número 24 na forma fatorada, devemos dividi-lo pelo primeiro número primo que seja possível, ou seja, dividir o número 24 por um número primo no qual a divisão seja exata.
Utilizando o algoritmo da divisão, vamos dividir o 24 por 2.
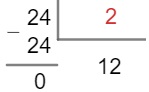
O quociente encontrado agora foi o número 12, então devemos dividi-lo novamente pelo primeiro número primo cuja divisão seja exata, ou seja, por 2.
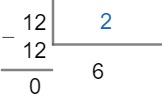
Devemos continuar esse processo até que o quociente seja igual a 1. Observe que agora o quociente é igual a 6, logo podemos dividi-lo por 2, pois o número 2 é o primeiro número primo no qual a divisão ainda é possível.
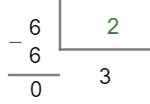
Note que o quociente agora é igual a 3, portanto não é possível dividi-lo por 2. Nesses casos, vamos dividi-lo pelo próximo número primo cuja divisão seja exata, ou seja, por 3.
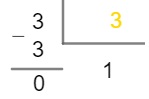
Como o quociente é igual a 1, a decomposição chegou ao fim, basta agora escrever os números primos (que estão dentro da chave) em forma de produto. Veja:
24 = 2 · 2 · 2 · 3
24 = 23 · 3
Veja que escrevemos o número 24 em forma de produto. Isso significa que fatoramos o número 24 utilizando números primos.
Escreva o número 25 em sua forma fatorada.
Nesse exemplo, vamos utilizar novamente o algoritmo da divisão, mas vamos escrevê-lo de maneira diferente, veja:
25 = 5 · 5 + 0
5 = 5 · 1 + 0
O número 25, na forma fatorada, é:
25 = 5 ·5
25 = 52
Leia também: Critérios de divisibilidade – processos que facilitam a operação de divisão
Observando o método anterior, se o número a ser fatorado for muito grande, como o número 1024, teremos algo bastante trabalhoso, pois serão necessárias sucessivas divisões por números primos até que o quociente seja igual a 1.
O método que veremos a seguir nada mais é do que uma simplificação da divisão. Em vez de escrever todos os elementos da divisão (divisor, dividendo, quociente e resto), vamos colocar somente o número primo pelo qual vamos dividir o número a ser fatorado e o quociente da divisão. Veja os exemplos:
Para fatorar o número 60, vamos seguir o mesmo passo a passo, mas vamos escrever somente o quociente da divisão (ou seja, o resultado) e o número primo pelo qual vamos dividir o número 60.
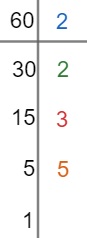
Veja que, ao dividir o 60 por 2, o resultado é 30 e, ao dividir o número 30 por 2, o resultado é 15, e assim sucessivamente até que o resultado da divisão seja igual a 1. O processo continua o mesmo, a única diferença está na simplificação de informações.
O número 60, em sua forma fatorada, é:
60 = 2 · 2 · 3 ·5
60 = 22 · 3 · 5

Questão 1 – Decomponha em fatores primos o número 192.
Resolução
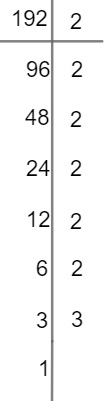
O número 192, em sua forma decomposta, é:
192 = 2 · 2 · 2 · 2 · 2 · 2 · 3
192 = 26 · 3
Questão 2 – Considere os números p e q tais que p = 25 · 5 e q = 32. Determine a razão entre q e p.
Resolução
A razão entre dois números é a divisão entre eles. Sempre devemos obedecer à ordem em que eles foram dados para fazer a divisão de q por p. Antes de realizar a divisão de fato, vamos fatorar o número q, buscando uma forma de simplificar o cálculo.
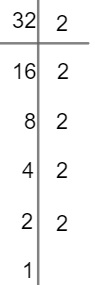
Temos que q = 32, logo podemos escrevê-lo desta forma:
q = 2 · 2 · 2 · 2 · 2
q = 25
Agora como fatoramos o número q, podemos montar a razão entre q e p e substituir os valores.
![]()