O número é chamado de primo quando ele é maior do que 1 e possui exatamente dois divisores: 1 e ele mesmo.

Chamamos de número primo um número natural que possui dois divisores: 1 e ele mesmo. Para encontrar números primos, foi desenvolvido o crivo de Eratóstenes. Quando um número não é primo, podemos escrevê-lo como a multiplicação de números primos, processo esse chamado de fatoração.
Leia também: Qual o valor de um algarismo?
A busca por números primos é bastante comum na Matemática. Quando dividimos um número por outro e o resultado é exato, ou seja, não deixa resto, esse número é chamado de divisor. Para identificar se um número é primo ou não, precisamos conhecer quais são os divisores desse número. Caso esse número tenha exatamente dois divisores: 1 e ele mesmo, ele é primo; caso contrário, não é primo.
|
Um número é chamado de primo quando possui exatamente dois divisores, 1 e ele mesmo. |
Exemplo
O número 12 não é primo, pois os números que dividem o 12 são:
D(12) = 1,2,3,4,6 e 12
Já o número 17 é primo, pois os divisores de 17 são:
D(17) = 1, 17.
Encontrar números primos nem sempre é uma tarefa fácil. O método mais usado para essa tarefa é o crivo de Eratóstenes, o qual permite encontrar todos os números primos entre dois números.
Vamos, por exemplo, encontrar os números primos de 1 até 100 utilizando esse método.
Listaremos todos os números de 1 até 100 de forma organizada. Veja:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
|
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
|
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
|
71 |
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
|
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
90 |
|
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
Sabemos que 1 possui só 1 divisor, então ele não é primo. Sabemos também que 2 possui 2 divisores, 1 e ele mesmo, então 2 é primo. Agora os demais números pares são todos divisíveis por 2, então eles não são primos. Assim, vamos marcar todos os outros números pares e o número 1 na lista.
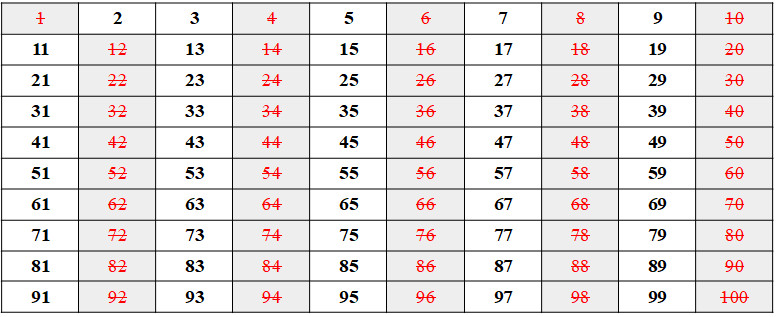
Dos números que restaram em preto, sabemos que 3 possui só dois divisores, logo ele é primo. Porém, os números múltiplos de 3, como o 6,9,12,15 …, não são primos. Marcaremos agora todos os números múltiplos de 3 que restaram na lista.
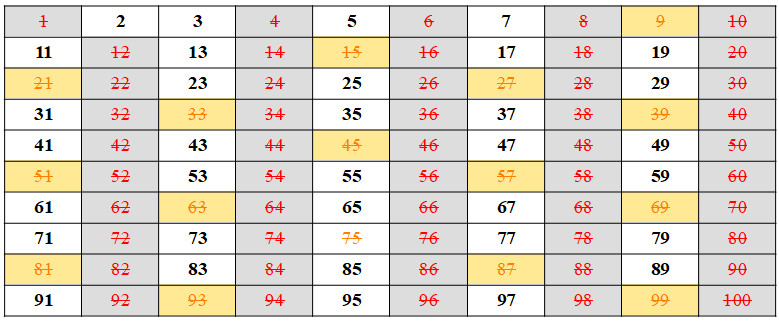
Sabemos que o número 5 é primo, mas os múltiplos de 5 (que são os números terminados em 5 ou 0) não são, pois 5 é divisor desses números. Então vamos marcar esses números também.
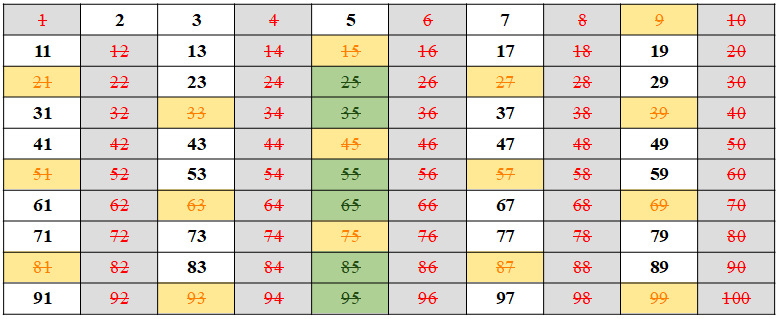
O número 7 é primo. Usando o mesmo raciocínio, marcaremos os múltiplos de 7 que ainda não foram assinalados.
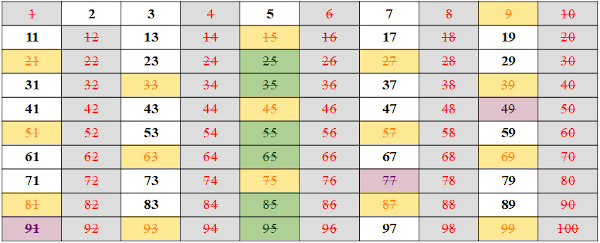
Agora sabendo que 11 é primo, vamos procurar os números múltiplos de 11, como não há nenhum número múltiplo de 11, sabemos que terminamos o crivo.
Os números restantes são primos, então os primos de 1 até 100 são: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 e 97.
Observação: Caso queiramos encontrar os primos entre números maiores, como os primos de 1 até 200 ou de 1 até 500, o processo continuará até encontrarmos um número primo que não possui nenhum múltiplo a ser riscado na tabela.
Veja também: Critérios de divisibilidade – processos que facilitam a operação de divisão
Um número que não é primo pode ser fatorado, ou seja, podemos realizar o que chamamos de decomposição de fatores primos. Esse processo é útil para calcular o MMC e o MDC.
Para fazer a decomposição, faremos divisões sucessivas do número até resultar em 1.

Então a decomposição de 72 em fatores primos é 2³.3².
Conheça todos os números primos que existem entre 1 e 1000.
|
2 |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
37 |
41 |
43 |
|
47 |
53 |
59 |
61 |
67 |
71 |
73 |
79 |
83 |
89 |
97 |
101 |
103 |
107 |
|
109 |
113 |
127 |
131 |
137 |
139 |
149 |
151 |
157 |
163 |
167 |
173 |
179 |
181 |
|
191 |
193 |
197 |
199 |
211 |
223 |
227 |
229 |
233 |
239 |
241 |
251 |
257 |
263 |
|
269 |
271 |
277 |
281 |
283 |
293 |
307 |
311 |
313 |
317 |
331 |
337 |
347 |
349 |
|
353 |
359 |
367 |
373 |
379 |
383 |
389 |
397 |
401 |
409 |
419 |
421 |
431 |
433 |
|
439 |
443 |
449 |
457 |
461 |
463 |
467 |
479 |
487 |
491 |
499 |
503 |
509 |
521 |
|
523 |
541 |
547 |
557 |
563 |
569 |
571 |
577 |
587 |
593 |
599 |
601 |
607 |
613 |
|
617 |
619 |
631 |
641 |
643 |
647 |
653 |
659 |
661 |
673 |
677 |
683 |
691 |
701 |
|
709 |
719 |
727 |
733 |
739 |
743 |
751 |
757 |
761 |
769 |
773 |
787 |
797 |
809 |
|
811 |
821 |
823 |
827 |
829 |
839 |
853 |
857 |
859 |
863 |
877 |
881 |
883 |
887 |
|
907 |
911 |
919 |
929 |
937 |
941 |
947 |
953 |
967 |
971 |
977 |
983 |
991 |
997 |
Questão 1 - A decomposição em fatores primos do número 720 é igual a?
A) 2³. 3². 5
B)2². 3³ . 5
C) 2 . 3. 5
D)2² . 3. 5³
Resolução
Alternativa A.
Realizando a fatoração, temos que:
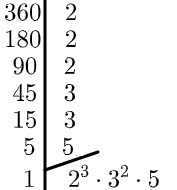
Questão 2 - Marque a afirmativa correta:
A) Todo número ímpar é primo.
B) Todo número par não é primo.
C) 2 é o único número par que é primo.
D) 9 é o único número ímpar que não é primo.
Resolução
Alternativa C.
a) Falsa, pois existem números primos e números não primos ímpares. Por exemplo, 3 é primo, mas 15 não.
b) Falsa, pois existe um único número par que é primo, o número 2.
c) Verdadeira, pois 2 é o único número par que é primo.
d) Falsa, pois existem vários outros números ímpares que não são primos, como o 15 citado, o 21, o 39, entre outros.