Multiplicação

Multiplicação é uma das operações básicas da Matemática. Multiplicação, adição, subtração e divisão são consideradas operações primárias por serem base para a realização de vários cálculos. Quando há a soma sucessiva de um número por ele mesmo, podemos reescrevê-la como uma multiplicação.

A multiplicação é representada pelo símbolo × ou por ⋅ entre dois números. Para encontrarmos o resultado de uma multiplicação, é importante conhecer a tabuada de multiplicação e dominar o algoritmo da multiplicação.

Veja também: Como realizar operações com frações?

Resumo sobre multiplicação:

• A multiplicação é uma das operações básicas da Matemática.
• A soma sucessiva dos números pode ser representada como uma multiplicação.
• O resultado da multiplicação é conhecido como produto.
• Para encontrar o produto entre dois números, utilizamos a tabuada e o algoritmo da multiplicação.
• São propriedades da multiplicação:
  • comutatividade;
  • associatividade;
  • distributividade;
  • existência de inverso;
  • existência de um elemento neutro.

Videoaula sobre multiplicação

Representação da multiplicação

A multiplicação é uma das operações básicas da Matemática que está diretamente ligada à adição. Em algumas situações, há a soma sucessiva de um número por ele mesmo. Dessa forma, podemos facilitar a escrita e a operação utilizando a multiplicação.

• Exemplo

Sabemos que:

\(2 + 2 + 2 + 2 + 2 + 2 + 2 = 14 \)

Essa adição sucessiva de 2 por ele mesmo 7 vezes pode ser representada por:

\( 2 × 7 = 14 \)

Podemos ler esse cálculo como “dois vezes sete”.

Termos da multiplicação

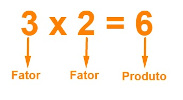
Em uma multiplicação entre dois números, estes são conhecidos como fatores. Já o resultado do cálculo é chamado de produto.

• Exemplo

Na multiplicação 3 x 2 = 6, temos:

Como calcular a multiplicação?

Para aprender a realizar a multiplicação entre dois números, primeiramente é necessário praticar a tabuada da multiplicação, a fim de que as multiplicações menores sejam conhecidas.

• Tabuada da multiplicação

Conhecendo as multiplicações que estão na tabuada, utilizamos um algoritmo conhecido como algoritmo da multiplicação para realizar a multiplicação entre números maiores.

• Exemplo 1

Calcule a multiplicação de \(32×4\).

Resolução:

De início, escreveremos a multiplicação com o maior fator em cima e o menor em baixo (não é uma regra, mas facilita o cálculo manual), deixando alinhadas as unidades, as dezenas e todos os algarismos.

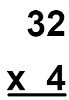
Agora, realizaremos a multiplicação de 4 por 2, com resultado 8, que será escrito na unidade do produto.

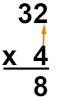
Por fim, realizaremos a multiplicação de 4 por 3, que é igual a 12. O resultado será escrito na frente do 8.

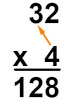
Assim, concluímos que:

\(32×4=128\)

• Exemplo 2

Calcule a multiplicação \(6×14\).

Resolução:

Montando a multiplicação:

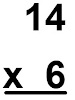
Multiplicando as unidades, constatamos que \(4×6=24\). Como o 2 é uma dezena, o escreveremos acima do 1 como na imagem a seguir:

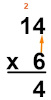
Agora, multiplicaremos \(6×1\) e somaremos 2 ao resultado. Sabemos que \(6×1=6\). Realizando a soma de 6 com 2, temos que \(6+2=8\).

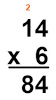
Então:

\(14×6=84 \)

• Exemplo 3

Calcule a multiplicação \(13×24\).

Resolução:

Montando a multiplicação:

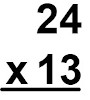
Sabemos que 4×3=12:

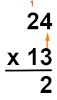
Agora, multiplicaremos 3 por 2 e somaremos 1 ao resultado. Sabemos que \(3×2=6\). Realizando a soma de 6 com 1, temos que \(6+1=7\).

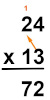
Desta vez, multiplicaremos 1 por 4. Neste caso, o resultado será escrito na unidade de dezena do número abaixo do 7.

A seguir, realizaremos a multiplicação de 1 por 2.

Por fim, somaremos os resultados encontrados:

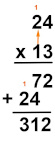
Portanto:

\(13×24=312 \)

Saiba mais: Qual é o algoritmo da divisão?

Propriedades da multiplicação

Veremos, a seguir, as principais propriedades da multiplicação.

• Propriedade comutativa

A propriedade comutativa determina que a ordem dos fatores não altera o produto, ou seja:

\(3×2=2×3=6\)

• Propriedade associativa

A propriedade associativa mostra que se tivermos uma multiplicação entre três números, a ordem da multiplicação não alterará o produto.

\((2×3)×4=2×(3×4) \)

\(6×4=2×12\)

\(24=24 \)

• Propriedade distributiva

Essa propriedade mistura a multiplicação e a adição. Resolvendo a expressão, temos:

\(2×3+4=2×3+2×4\)

\(2×7=6+8 \)

\(14=14\)

• Existência de um elemento neutro

Na multiplicação existe um número neutro, que é o 1, pois qualquer número multiplicado por 1 será ele mesmo. Exemplo:

\(2×1=2 \)

Exercícios resolvidos sobre multiplicação

Questão 1

Em uma sala de aula há 6 fileiras de cadeiras com 7 cadeiras cada. O número de cadeiras que existem nessa sala de aula é:

A) 13

B) 26

C) 30

D) 42

Resolução:

Alternativa D

Para calcular o total de cadeiras, basta multiplicar 7 por 6:

\(7×6=42\)

Há um total de 42 cadeiras na sala.

Questão 2

Um analista de processos de trânsito gasta 12 minutos para analisar cada processo. Se em um dia a demanda foi de 25 processos, o tempo gasto para ele analisar o total foi de:

A) 120 minutos

B) 180 minutos

C) 240 minutos

D) 300 minutos

Resolução:

Alternativa D

Calculando a multiplicação:

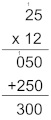
Foram gastos 300 minutos.