O teorema de Pitágoras relaciona as medidas dos lados de um triângulo retângulo. Seu enunciado é: o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
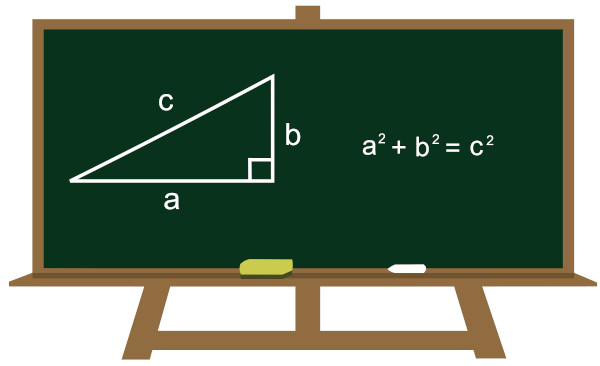
O teorema de Pitágoras é uma relação matemática entre as medidas dos lados de um triângulo retângulo. Esse teorema está sintetizado na frase: o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
Leia também: Como se classifica os triângulos?
\(a^2+b^2=c^{2}\)
O teorema de Pitágoras é válido para todos os triângulos retângulos. Lembre-se de que um triângulo retângulo apresenta um ângulo interno de 90°, chamado de ângulo reto. Os lados do triângulo retângulo que formam o ângulo de 90° são os catetos, e o terceiro lado é a hipotenusa.
Considere um triângulo retângulo em que os catetos medem a e b e a hipotenusa mede c. A fórmula do teorema de Pitágoras determina que
\(a^2+b^2=c^{2}\)
Curiosidade: Neste tópico, afirmamos que se um triângulo é retângulo então a fórmula do teorema de Pitágoras pode ser aplicada, mas você sabia que a ideia inversa também é verdadeira? Em um triângulo qualquer, se o teorema de Pitágoras é válido, então esse triângulo é, necessariamente, um triângulo retângulo. Esse raciocínio é chamado de recíproca do teorema de Pitágoras.
Para utilizar o teorema de Pitágoras, precisamos identificar as medidas dos catetos e da hipotenusa e aplicar a fórmula. Perceba que podemos utilizar a fórmula do teorema de Pitágoras tanto para encontrar a medida da hipotenusa (com base nas medidas dos catetos) como para encontrar a medida de um cateto (com base nas medidas do outro cateto e da hipotenusa).
Em cada exemplo, vamos determinar a medida do lado desconhecido.
Exemplo 1:
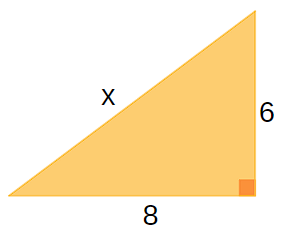
Note que 6 e 8 são as medidas dos catetos e x é a medida da hipotenusa. Aplicando na fórmula do teorema de Pitágoras:
\(6^2+8^2=x^2\)
\(36+64=x^2\)
\(100=x^2\)
Como a medida x da hipotenusa é um número positivo, concluímos que:
\(x=10\)
Exemplo 2:
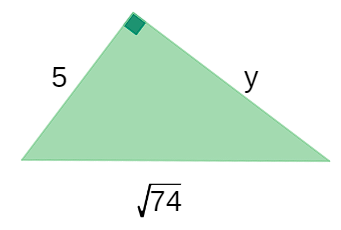
Perceba que, neste caso, a medida desconhecida é de um dos catetos. O outro cateto mede 5 e a hipotenusa mede \(\sqrt{74}\). Atenção para a aplicação da fórmula do teorema de Pitágoras:
\(5^2+y^2=\left(\sqrt{74}\right)^2\)
\(25+y^2=74\)
\(y^2=74-25\)
\(y^2=49\)
Como a medida y do cateto é um número positivo, concluímos que:
\(y=7\)
Veja também: O que é um triângulo equilátero?
Todo teorema precisa ser justificado por argumentos matemáticos. Essa justificativa é chamada de prova ou demonstração matemática e consiste em uma sequência de raciocínios que se concluem ao obter-se a fórmula do teorema. No caso do teorema de Pitágoras, há dezenas de maneiras de demonstrá-lo.
A seguir, vamos conhecer uma demonstração que utiliza área de triângulos e de trapézios.
Considere um trapézio retângulo de base maior b, base menor a e altura b+a. Decomponha esse trapézio em três triângulos, sendo dois triângulos retângulos com catetos b e a e hipotenusa c, conforme a imagem. Com base nessa construção, note que esses dois triângulos são congruentes pelo caso LLL. Consequentemente, analisando os ângulos, temos que o triângulo no meio também é retângulo.
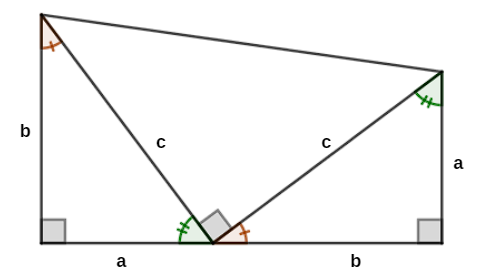
Perceba que a soma das áreas dos triângulos é igual à área do trapézio. Assim,
\(A_{total triângulos}=b⋅a2+c⋅c2+b⋅a2=2ab+c22\)
\(A_{trapézio}=b+a⋅b+a2=b2+2ab+a22\)
Logo:
\(A_{total triângulos}=A_{trapézio}\)
\(\frac{2ab+c^2}{2}=\frac{b^2+2ab+a^2}{2}\)
\(c^2=a^2+b^2\)
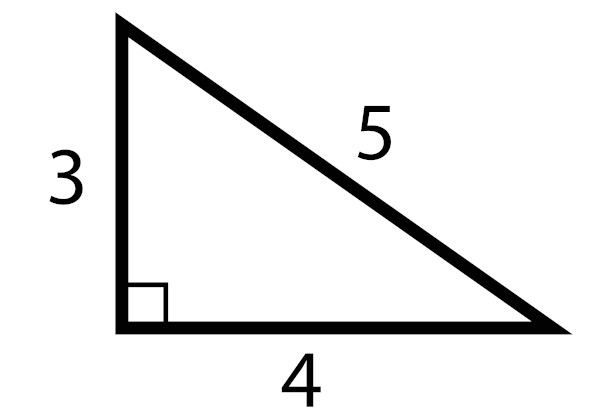
Um triângulo retângulo é chamado de pitagórico se as medidas de todos os lados são números inteiros. O triângulo pitagórico mais famoso é o “3, 4 e 5”, em que os catetos medem 3 e 4 e a hipotenusa mede 5.
Ao aplicar o teorema de Pitágoras para descobrir um dos lados de um triângulo retângulo, é comum nos depararmos com números irracionais. Lembre-se de que os números irracionais são números com infinitas casas decimais não periódicas.
Exemplo:
Qual a medida da hipotenusa de um triângulo retângulo em que os dois catetos medem 1 cm?
Vamos chamar de a e b as medidas dos catetos desse triângulo retângulo e de c a medida da hipotenusa. Assim, a = 1 cm e b = 1 cm. Aplicando a fórmula do teorema de Pitágoras, temos que:
\(a^2+b^2=c^2\)
\(1^2+1^2=c^2\)
\(2=c^2\)
\(c=\sqrt2 cm\)
Concluímos que a medida da hipotenusa é um número irracional. Observe que isso acontece ainda que os dois catetos sejam números racionais.
Saiba mais: Como se calcula a área de um quadrado?

Pitágoras de Samos foi um filósofo, matemático e astrônomo grego. Seus estudos e de seus aprendizes na Escola Pitagórica se baseavam na ideia de que “O princípio de tudo é o número”, ou seja, de que o mundo seria regido por números.
É importante destacar que a Escola Pitagórica possuía um aspecto religioso. Assim, a Matemática era percebida por uma ótica mística e não científica.
Questão 1
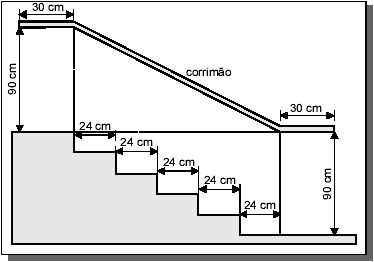
(Enem) Na figura abaixo, que representa o projeto de uma escada de 5 degraus de mesma altura, o comprimento total do corrimão é igual a:
a) 1,8 m
b) 1,9 m
c) 2,0 m
d) 2,1 m
e) 2,2 m
Resolução
Perceba que o corrimão possui dois trechos menores de 30 cm e um trecho maior de medida desconhecida. Esse trecho maior é a hipotenusa de um triângulo retângulo com catetos medindo 90 cm e 120 cm (24⋅5=120).
Chamando a medida do trecho maior de x e aplicando o teorema de Pitágoras:
\({90}^2+{120}^2=x^2\)
\(x=150 cm\)
Portanto, ao todo, o corrimão mede \(30+30+150=210\ cm=2,1\ m\).
Alternativa D
Questão 2
(Enem) A unidade de medida utilizada para anunciar o tamanho das telas de televisores no Brasil é a polegada, que corresponde a 2,54 cm. Diferentemente do que muitos imaginam, dizer que a tela de uma TV tem X polegadas significa que a diagonal do retângulo que representa sua tela mede X polegadas, conforme ilustração.
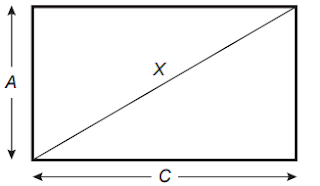
O administrador de um museu recebeu uma TV convencional de 20 polegadas, que tem como razão do comprimento (C) pela altura (A) a proporção 4 : 3, e precisa calcular o comprimento (C) dessa TV a fim de colocá-la em uma estante para exposição.
A tela dessa TV tem medida do comprimento C, em centímetro, igual a
a) 12,00.
b) 16,00.
c) 30,48.
d) 40,64.
e) 50,80.
Resolução
Como a razão do comprimento (C) pela altura (A) corresponde à proporção 4 : 3, temos que:
\(\frac{C}{A}=\frac{4}{3}\)
Ou seja:
\(A=\frac{3}{4}C\)
Na imagem, temos que X é a hipotenusa de um triângulo retângulo de medidas A e C. Pelo teorema de Pitágoras:
\(X^2=A^2+C^2\)
Substituindo X = 20 polegadas e \(A=\frac{3}{4}C\), obtemos a expressão:
\({20}^2=\left(\frac{3}{4}C\right)^2+C^2\)
\(400=\frac{9}{16}C^2+C^2\)
\(400=\frac{25}{16}C^2\)
\(C^2=\frac{400\cdot16}{25}\)
\(C^2=256\)
\(C=16 polegadas\)
Como 1 polegada corresponde a 2,54 cm, então:
\(C=16\cdot2,54=40,64 cm\)
Alternativa D
Fontes
5 demonstrações do Teorema de Pitágoras. Derivando a Matemática. Disponível em: http://www.ime.unicamp.br/~apmat/5-demonstracoes-do-teorema-de-pitagoras/.
GOLÇALVES, Carlos H.B.; POSSANI, Claudio. Revisitando a descoberta dos incomensuráveis na Grécia Antiga. Matemática Universitária (SBM). Rio de Janeiro, nº 47, p. 16 a 24. Disponível em: https://rmu.sbm.org.br/wp-content/uploads/sites/27/2018/03/n47_Artigo02.pdf.