O triângulo equilátero é uma figura geométrica plana que possui como principal característica os três lados congruentes, ou seja, a medida desses três lados é a mesma.
Esse fato gera uma consequência imediata, os três ângulos internos desse triângulo também são iguais entre si. Além disso, esse triângulo possui importantes propriedades geométricas que facilitam a resolução de determinadas situações-problemas.
Leia também: Qual é a condição de existência de um triângulo?
O triângulo equilátero possui algumas propriedades que facilitam a resolução de algumas situações-problemas.
Propriedade 1 – Todos os ângulos internos de um triângulo equilátero medem 60°.
Propriedade 2 – A altura (segmento perpendicular a um dos lados), a mediana (segmento que divide um lado ao meio) e a bissetriz (segmento que divide um ângulo ao meio) coincidem-se.
Sabemos que o perímetro de um polígono qualquer é dado pela soma das medidas de todos os lados, e no triângulo equilátero, a ideia não é diferente. Pelo fato do triângulo equilátero possuir todos os lados iguais, podemos determinar uma fórmula que facilite o cálculo do perímetro.
Considere um triângulo equilátero de lado l:
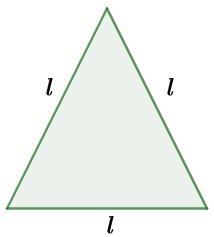
Como o perímetro é dado pela soma de todos os lados, então:
2P = l + l + l
2P = 3 · l
Lembre-se: a notação para perímetro é 2P. Utilizamos a letra P para representar o semiperímetro. A fórmula afirma que para calcular o perímetro de um triângulo equilátero basta multiplicar a medida do lado por 3.
Determine o perímetro do triângulo equilátero cujo lado é de 4 cm.
Substituindo o valor do lado na fórmula deduzida, temos:
2P = 3 · l
2P = 3 · 4
2P = 12 cm
Portanto, o perímetro é de 12 centímetros.
Leia também: Semelhança de triângulos: quais são os casos?
Para calcular a área de um triângulo equilátero, inicialmente traçamos a altura relativa a um dos lados. Pelas propriedades sabemos que a altura coincide com a mediana, ou seja, ao traçar a altura, divide-se o lado pela metade.
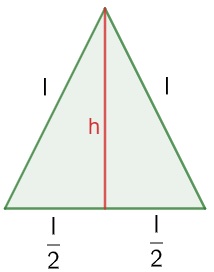
Sabemos que a área de qualquer triângulo é dada pela multiplicação da base com a altura, e isso dividido por 2.
![]()
Observe que o valor da base é conhecido no caso l, entretanto o valor da altura é desconhecido. Desse modo, para determinar a área do triângulo equilátero, é necessário, antes, encontrar a altura dele. Para isso, utilizaremos o teorema de Pitágoras:

Como agora conhecemos a medida da altura, podemos substituir na fórmula da área de um triângulo.
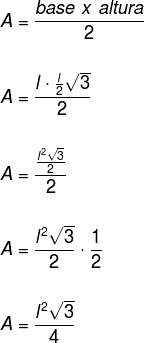
Determine a área do triângulo equilátero cujo lado mede 4 cm.
Para calcular a área de um triângulo equilátero, basta substituir a medida do lado na fórmula, sabendo que, nela, l representa essa medida. Assim temos:


Questão 1 – Um fazendeiro precisou construir um cercado para que sua criação de galinhas não fugisse. Ao fazer o projeto, notou que o cercado ficaria em forma de um triângulo equilátero com 3 metros de comprimento de lado. Quantos metros de cerca esse fazendeiro terá que comprar? Sabendo que cada metro custa 4 reais e 50 centavos, quanto ele gastará?
Resolução
O terreno do fazendeiro pode ser representado por:
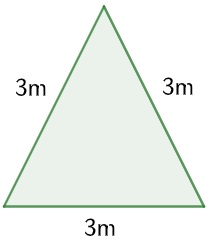
O perímetro é dado por:
2P = 3 · 3
2P = 9 m
Como cada metro custa 4,50 reais, o fazendeiro gastará 9 vezes esse valor:
gasto = 4,5 · 9
gasto = 40,5
Portanto, o fazendeiro gastará 40 reais e 50 centavos.
Questão 2 – Uma empresa de azulejos precisa cobrir o fundo de uma piscina com azulejos de 1 m2. A piscina tem o formato de um triângulo equilátero de lado de 6 metros. Determine a quantidade de azulejos a ser utilizada.
(Dado: Use √3 = 1,7)
Resolução
Inicialmente determinamos a área da piscina.

Como cada azulejo tem 1 m2, então terão que ser comprados 16 azulejos, uma vez que não se vende 0,3 azulejo.