Perímetro de um polígono

Perímetro e polígono são dois conceitos que estudamos desde os primeiros anos de nossa vida escolar, não é mesmo? Dessa vez, a fim de aprender a medir perímetros de polígonos, relacionaremos esses dois conceitos matemáticos. Para isso vamos relembrar o que é cada um deles.

O perímetro é o comprimento da linha ou do contorno de uma determinada figura (polígono). Ou ainda, é a soma das medidas dos lados de um polígono.

Polígonos são figuras fechadas formadas por segmentos de reta e caracterizam-se pelos seguintes elementos: ângulos, vértices, diagonais e lados.

Esses dois conceitos, citados de forma simples, são suficientes para que possamos compreender o cálculo do perímetro de um polígono. Portanto, para calcularmos o perímetro de qualquer polígono precisamos apenas somar a medida dos lados desse polígono.

Assim, vejamos como fazer o cálculo desse perímetro em um problema que envolve polígonos.

“Um milionário construiu sua casa em um condomínio de luxo. Ele deseja cercar o lote em que construiu sua mansão. Veja a vista panorâmica desse lote e calcule quantos metros de cerca ele deverá comprar.”

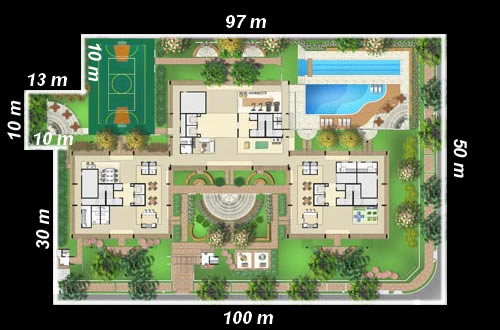
Vimos em nosso estudo que perímetro é o comprimento do contorno de uma figura. A cerca que o milionário deseja colocar fará justamente um contorno em seu lote, portanto é preciso calcular o perímetro de seu lote.

E o perímetro nós sabemos calcular, certo? Como dito, devemos somar a medida dos lados desse polígono.

Assim sendo, devemos realizar os seguintes cálculos:

Portanto, o perímetro desse lote é de 320 metros e com isso podemos afirmar que serão necessários 320 metros de cerca para cercar o lote do milionário.

Veja que o perímetro utiliza apenas a ideia da adição de medidas, algo fácil e que está presente em nosso cotidiano.

Por Gabriel Alessandro de Oliveira
Graduado em Matemática
Equipe EscolaKids