Polígonos são figuras geométricas planas e fechadas delimitadas por segmentos de reta. Alguns exemplos de polígono são os triângulos, os quadrados e os retângulos.
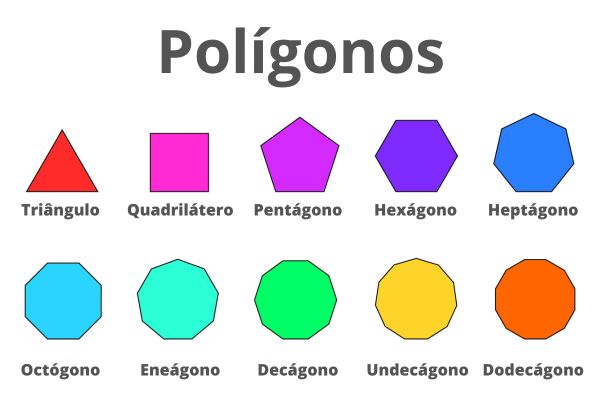
Polígonos são figuras geométricas planas e fechadas formadas por segmentos de reta que se encontram nas extremidades. Cada segmento é um lado do polígono, e o ponto de encontro de dois segmentos adjacentes é um vértice.
Triângulos, quadrados, retângulos, losangos e pentágonos são alguns exemplos de polígonos. Já a circunferência e o círculo não são polígonos, pois são formados por curvas, e não por segmentos de reta.
Leia também: Polígonos inscritos e circunscritos e seus principais elementos e propriedades
\(S_n=\left(n-2\right)\cdot180°\)
Polígonos são figuras geométricas planas e fechadas formadas por segmentos de reta que se interceptam apenas nas extremidades. A palavra polígono tem origem grega: póly (vários) e gonía (ângulos). Veja a seguir alguns exemplos de figuras que são polígonos:
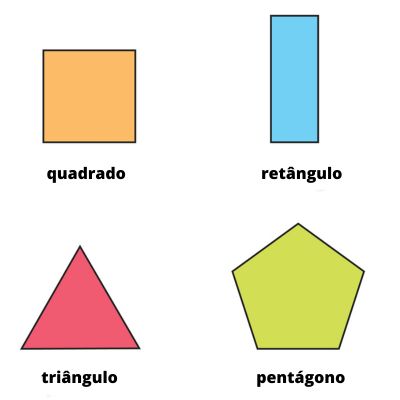
Importante: se são considerados polígonos as figuras que possuem as características acima, não são classificadas como polígonos as figuras abertas, fechadas com segmentos que se interceptam fora das extremidades e fechadas de contornos curvos. Veja a seguir alguns exemplos de figuras que não são polígonos:

Os principais elementos de um polígono são os lados, os vértices e os ângulos internos. Além deles, outros elementos importantes são os ângulos externos e as diagonais. Veja sobre cada um deles a seguir.
Observe o triângulo ABC abaixo, polígono no qual os vértices são A, B e C; os lados são \(\overline{AB},\overline{BC}\) e \(\overline{CA}\); os ângulos são \(\hat{A}\), \(\hat{B}\) e \(\hat{C}\) .


Importante: o número de vértices, lados e ângulos (internos e externos) de um polígono é o mesmo. Assim, um polígono de n lados terá n vértices, n ângulos internos e n ângulos externos.

As principais classificações de polígonos são: polígonos convexos e polígonos regulares.
Polígono convexo é o polígono em que, dados dois pontos que pertencem ao polígono, o segmento que une esses pontos também pertence ao polígono. Na imagem abaixo, o polígono que está à sua esquerda é convexo, enquanto o polígono que está à sua direita não é convexo.

Polígono regular é o polígono em que todos os lados e ângulos (internos e externos) são congruentes (ou seja, possuem a mesma medida). Por exemplo, um triângulo regular é chamado de triângulo equilátero e possui 3 ângulos internos de 60°. Na imagem abaixo, o polígono à esquerda é um quadrilátero regular (quadrado), enquanto o polígono à direita é um quadrilátero não regular (nesse caso, um retângulo).

O nome de um polígono de três lados é triângulo e de quatro lados é quadrilátero. Existem diferentes tipos de quadriláteros, como o quadrado, o retângulo, o losango e o trapézio. Já a nomenclatura para polígonos com 5 lados ou mais segue um padrão. A primeira parte do nome se refere à quantidade de lados, e a segunda parte é o termo grego gono. Veja:
5 lados – pentágono
6 lados – hexágono
7 lados – heptágono
8 lados – octógono
9 lados – eneágono
10 lados – decágono
O perímetro de um polígono é a soma das medidas de seus lados.
Os lados de um triângulo medem 3 cm, 4 cm e 5 cm. Qual o perímetro desse polígono?
Resolução:
O perímetro do triângulo é 12 cm, pois
\(3\ +\ 4\ +\ 5\ =\ 12\)
A área de um polígono é a medida de sua superfície. Alguns polígonos simples possuem fórmulas próprias para o cálculo de sua área. A imagem a seguir apresenta algumas dessas expressões.

Qual a área de um terreno retangular com 15 m de comprimento e 12 m de largura?
Resolução:
A área desse terreno é igual a 180 m², pois
\(A_{retângulo}=15m⋅12m=180 m^2\)
Outros polígonos que também possuem fórmulas específicas para o cálculo da área são o trapézio, o losango e os polígonos regulares, como o pentágono regular, hexágono regular, heptágono regular, etc.
Para calcular a área de polígonos menos usuais, devemos repartir sua superfície em formatos mais comuns. Assim, a área do polígono será uma soma de áreas conhecidas.
Calcule a área do polígono abaixo.

Resolução:
Note que esse polígono pode ser repartido em duas regiões: uma superior e uma inferior. A região superior é um retângulo cujos lados medem 2 e 5, e a região inferior é um quadrado de lado 2.

Assim, a área desse polígono é a soma da área do retângulo e da área do quadrado:
\(A=\left(5\cdot2\right)+\left(2^2\right)\)
\(A\ =14\)
A soma Sn dos ângulos internos de um polígono convexo com n lados é dada por:
\(S_n=\left(n-2\right)\cdot180°\)
Qual a soma dos ângulos internos de um pentágono?
Resolução:
Como o pentágono é um polígono com 5 lados, temos
\(S_5=\left(5-2\right)\cdot180°\)
\(S_5=540°\)
A soma dos ângulos externos de um polígono convexo é sempre igual a 360°, independentemente do número de lados do polígono.
Veja também: Poliedros — os sólidos geométricos que possuem todas as suas faces formadas por polígonos
Questão 1
O perímetro de um quadrado mede 52 cm. A área desse quadrado é, em cm², igual a
A) 130
B) 169
C) 260
D) 520
E) 676
Resolução:
Alternativa B.
Um quadrado possui quatro lados de tamanho l . Assim,
\(Perímetro=4⋅l\)
\(52\ =\ 4\cdot l\)
\(l=\frac{52}{4}=13 cm\)
Portanto,
\(Área=l^2\)
\(Área=13^2=169 cm^2\)
Questão 2
(Faap) A medida mais próxima de cada ângulo externo do heptágono regular da moeda de R$ 0,25 é:

A) 60°
B) 45°
C) 36°
D) 83°
E) 51°
Resolução:
Alternativa E.
Um heptágono regular possui 7 ângulos externos congruentes. Como a soma dos ângulos é 360°, a medida de cada ângulo externo α é
\(\alpha=\frac{360°}7≈51,43\)
Fontes
LIMA, E. L. Geometria Analítica e Álgebra Linear. Rio de Janeiro: IMPA, 2014.
REZENDE, E.Q.F.; QUEIROZ, M. L. B. de. Geometria Euclidiana Plana: e construções geométricas. 2ª ed. Campinas: Unicamp, 2008.