Cubo

O cubo é um sólido geométrico pertencente à classe dos poliedros e cuja característica principal é possuir seis faces compostas por quadrados congruentes, ou seja, com lados de mesma medida. Com base na medida do lado de um cubo, é possível calcular a sua diagonal, a área total de suas faces e a sua capacidade volumétrica.

Leia também: Prisma — poliedro que possui duas bases poligonais idênticas e áreas laterais retangulares ligando uma base à outra

Resumo sobre o cubo

• O cubo é um poliedro composto de seis faces quadradas de mesma medida.
• Ele possui seis faces, oito vértices e 12 arestas.
• A diagonal interna de um cubo de lado a é calculada pela seguinte fórmula:

$D=a\sqrt3$

• A área total da superfície de um cubo é dada pela seguinte fórmula:

$A=6\cdot a^2$

• O volume de um cubo de lado a é calculado pela seguinte fórmula:

$V=a^3$

O que é cubo?

O cubo é um poliedro que possui seis faces quadradas congruentes entre si, ou seja, quadrados que possuem a mesma medida de lado.  Desse modo, o cubo também pode ser chamado de hexaedro regular, pois possui seis faces cujas arestas têm todas a mesma medida.

Composição do cubo

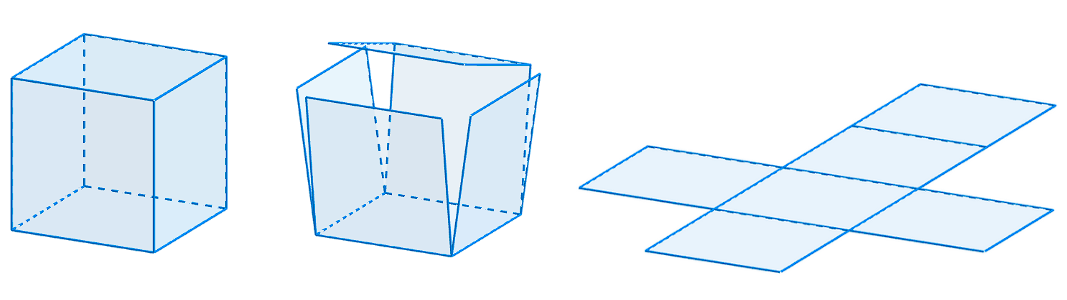
Assim como em outros poliedros, é possível destacar alguns elementos que compõem o cubo. No caso, ele possui seis faces, 12 arestas e oito vértices:

No cubo acima, é possível destacar os seguintes elementos:

• Faces: são as superfícies planas quadradas que compõem o cubo. São representadas pelos quadrados: ABCD, ADEH, ABGH, BCFG, CDEF e EFGH.
• Arestas: são as linhas que representam o encontro entre duas faces do cubo. São representadas pelos segmentos $\bar{AB},\ \bar{BC},\ \bar{CD},\ \bar{DA},\ \bar{GH},\ \bar{HE},\ \bar{EF},\ \bar{FG},\ \bar{AH},\ \bar{BG},\ \bar{DE} \ e\ \bar{CF}.$.
• Vértices: são os pontos que unem as arestas do cubo. São representados pelos pontos A, B, C, D, E, F, G e H.

Diagonais do cubo

Também chamada de diagonal interna do cubo, a diagonal de um cubo é um segmento que liga dois vértices do cubo que estão em faces opostas, de modo que esse segmento esteja contido no interior do cubo (não pertencendo a nenhuma de suas faces).

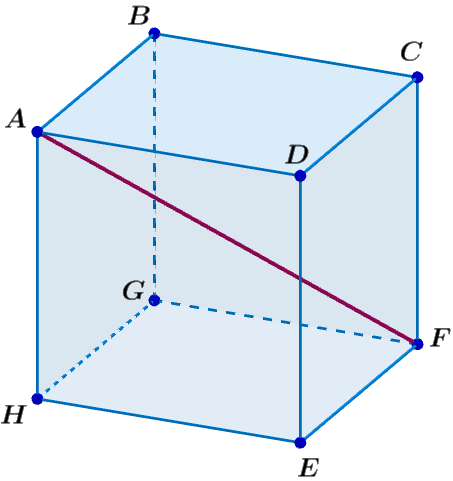
Conhecendo a medida de uma das arestas do cubo, é possível determinar a medida da diagonal interna do cubo por meio do teorema de Pitágoras. Isso ocorre porque a diagonal interna do cubo pode ser vista como a hipotenusa de um triângulo retângulo cujos catetos são uma das arestas do cubo (na imagem a seguir representada por $\bar{AH}$) e a diagonal de uma das faces desse sólido (representada por $\bar{HF}$):

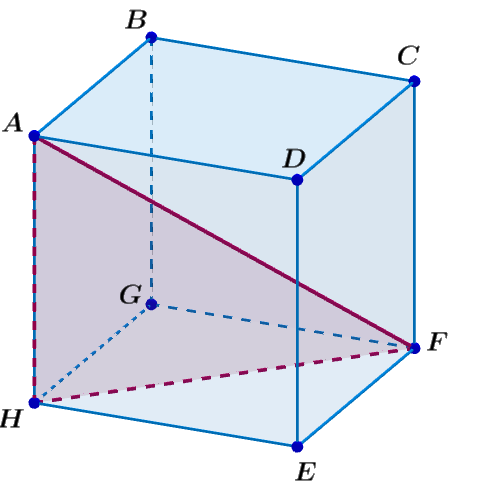
Também chamada de diagonal lateral do cubo, a diagonal de uma das faces do cubo é a diagonal de um quadrado. Assim, se o lado do quadrado tiver medida a:

$Diagonal \ do\ quadrado =a\sqrt2$

Desse modo, em um cubo de aresta de medida a, sua diagonal interna é calculada por meio do teorema de Pitágoras:

$\left(hipotenusa\right)^2=\left(cateto_1\right)^2+\left(cateto_2\right)^2$

$\left(diagonal\ interna\ do\ cubo\right)^2=\left(aresta\ do\ cubo\right)^2+\left(diagonal\ de\ um\ quadrado\right)^2$

$\left(\bar{AF}\right)^2=\left(\bar{AH}\right)^2+\left(\bar{HF}\right)^2$

$\left(\bar{AF}\right)^2=\left(a\right)^2+\left(a\sqrt2\right)^2$

$\left(\bar{AF}\right)^2=a^2+2a^2$

$\left(\bar{AF}\right)^2={3a}^2$

$\bar{AF}=\sqrt{3a^2}$

$\bar{AF}=a\sqrt3$

Logo, um cubo de aresta a possui a seguinte medida da diagonal interna:

$diagonal\ interna\ do\ cubo=a\sqrt3$

Veja também: Quadrado — polígono que possui quatro lados e quatro ângulos com a mesma medida

Quais são as fórmulas do cubo

Conhecendo a medida de uma das arestas de um cubo, é possível calcular a medida da área total de sua superfície e o seu volume.

→ Área do cubo

A área total do cubo refere-se à área superficial total desse sólido, ou seja, é a soma da área de todas as faces que o compõem.

Como todas as faces do cubo são quadrados de mesma medida de lado, então a área total do cubo é igual a seis vezes a área de uma de suas faces.

Assim, um cubo cuja aresta mede a possui a seguinte área total:

$área\ total\ do\ cubo=6\cdot(área\ de \ uma\ das \ faces)$

$área\ total\ do\ cubo=6\cdot a^2$

→ Volume do cubo

O volume de um cubo é a medida do espaço que ele ocupa. Para calcular o volume de um cubo, basta multiplicar a área de uma de suas faces pela sua altura.

Como em um cubo a área de uma das faces é a área de um quadrado e sua altura é igual à medida de uma de suas arestas, então seu volume é dado por:

$volume\ do\ cubo=(área \ de\ uma \ das \ faces)\cdot(altura \ do \ cubo)$

$volume\ do\ cubo=(área \ de\ um\ quadrado)\cdot a$

$volume\ do\ cubo=a^2 \cdot a$

$volume\ do\ cubo=a^3$

Para saber mais sobre o volume do cubo, clique aqui.

Exercícios resolvidos sobre cubo

Questão 1

Joana sabe que a soma da medida de todas as arestas de um cubo que ela tem em casa é igual a 60 cm. Qual é a medida de cada aresta do cubo de Joana?

A) 5 cm

B) 6 cm

C) 10 cm

D) 12 cm

Resolução:

Alternativa A

Sabe-se que um cubo é um sólido geométrico em que todas as suas arestas possuem a mesma medida. Além disso, o cubo possui um total de 12 arestas.

Assim, a medida de cada aresta é de:

$\frac{soma\ da\ medida\ das\ arestas}{total\ de\ arestas}=\frac{60\ cm}{12}=5\ cm$

Questão 2

Caio foi contratado para construir uma escultura com o formato de um cubo. Foi pedido a ele que a diagonal interna da escultura tenha uma medida de 53 dm. Qual o volume da escultura que deve ser construída por Caio?

A) 25 dm³

B) 60 dm³

C) 75 dm³

D) 125 dm³

Resolução:

Alternativa D

Sabendo o valor da diagonal de um cubo, é possível determinar a medida da aresta desse sólido:

$diagonal\ interna\ do\ cubo=a\sqrt3$

$5\sqrt3\ dm=a\sqrt3$

$a=5\ dm$

Assim, conhecendo a medida da aresta do cubo, é possível determinar seu volume por meio da fórmula:

$volume\ do\ cubo=a^3$

$volume\ do\ cubo={(5\ dm)}^3$

$volume\ do\ cubo=125\ dm^3$

Fontes

ALMEIDA, Célio Pinto de. Geometria espacial. 1. ed. Rio de Janeiro: G. Ermakoff, 2018.

DOLCE, Osvaldo; NICOLAU, José. Fundamentos de matemática elementar 10 – Geometria espacial. 5. ed. Santos: Atual, 1993.