O prisma é um sólido geométrico formado por duas bases congruentes pertencentes a planos paralelos e pela ligação dos vértices correspondentes a essas bases.

O prisma é um sólido geométrico que estudamos na Geometria Espacial. No nosso dia a dia, há vários objetos que possuem formato de prisma. É considerado prisma o poliedro que possui duas bases formadas por polígonos iguais e áreas laterais retangulares ligando o vértice de uma base ao seu correspondente na outra base.
Esse poliedro pode ser classificado como reto ou oblíquo, dependendo do seu formato, pois quando inclinado, ele é conhecido como prisma oblíquo. Caso contrário, é um prisma reto. As caixas, de forma geral, possuem formato de prisma, assim como prédios e outros elementos do cotidiano.
Existem diferentes tipos de prisma, pois como a sua base pode ser qualquer polígono, pode haver prismas de base triangular, quadrangular, pentagonal, hexagonal, entre outros. O mais comum deles é o prisma de base quadrangular, conhecido também como paralelepípedo retângulo. Os principais elementos do prisma são as suas faces, os seus vértices e as suas arestas. Existem fórmulas específicas para o cálculo do volume e da área total do prisma.
Leia também: Como se dá a planificação de um sólido geométrico?
\(AT=2A_b+Al\)
\(V=A_b\cdot h\)
Assim como os demais poliedros, o prisma é composto pelos vértices, arestas e faces, seus principais elementos. Vale destacar que ele possui como característica faces laterais formadas por paralelogramos e bases formadas por quaisquer polígonos.

Há diferentes tipos de prisma, dependendo do formato da sua base. Existem prismas de base triangular, quadrada, quadrangular, pentagonal, hexagonal, entre outros. O prisma pode ser formado por qualquer base, desde que ela seja um polígono. Veja, a seguir, os principais tipos de prisma.

O prisma pode ser considerado um prisma reto ou um prisma oblíquo.

Para calcular a área lateral, a área total e o volume do prisma, utilizamos fórmulas específicas. Vejamos, a seguir, cada uma delas.
A área lateral do prisma reto é um retângulo e do prisma oblíquo é um paralelogramo. Em ambos os casos, calculamos a área multiplicando a base pela altura, mas a área lateral depende do polígono que forma a base do prisma. Sendo \(A_1\), \(A_2\), ..., \(A_n\) a área de cada face lateral do prisma com uma base de n lados, a área lateral é dada por:
\(A_l=A_1+A_2+...\ A_n\)
Analise o prisma a seguir e calcule sua área lateral.
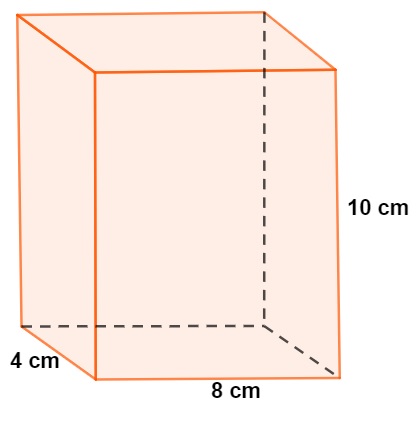
Resolução:
A área lateral desse prisma é composta por 4 retângulos, 2 de lados medindo 4 cm e 10 cm e 2 de lados medindo 8 cm e 10 cm.
Assim, podemos calcular a área lateral da seguinte maneira:
\(A_l=2\cdot4\cdot10+2\cdot8\cdot10\)
\(A_l=80+160\)
\(A_l=240cm^2\)
Veja também: Como se calcula a área do cilindro?
Conhecendo a área lateral do prisma, sabemos que ele possui duas bases iguais, formadas por polígonos. Então, para calcular a área total, é necessário calcular a área das bases mais a área lateral.
\(AT=2Ab+Al\)
A partir da análise do mesmo prisma utilizado para o cálculo da área lateral, calcule a área total.
Resolução:
A área total é encontrada por meio da soma das áreas das bases com a área lateral. As bases são retângulos, e a área é igual ao produto das dimensões da base. Ou seja:
\(A_b=4\cdot8=32cm²\)
Portanto, a área total será:
\(A_T=2A_b+A_l\)
\(A_T=2\cdot32+240\)
\(A_T=64+240\)
\(A_T=304\ cm^2\)
O volume do prisma é igual ao produto da área da base pela altura, quer ele seja oblíquo ou reto.
\(V=A_b·h\)
A partir da análise do mesmo prisma utilizado para o cálculo da área lateral e da área total, calcule o volume.
Resolução:
Sabemos que a sua base é de 32 cm². Para calcular o volume, basta multiplicar a área da base pela altura, que é de 10 cm. Logo, temos que:
\(V=A_b\cdot h\)
\(V=32\cdot10\)
\(V=320\ cm^3\)
Questão 1
(Enem 2017) Uma rede hoteleira dispõe de cabanas simples na ilha de Gotland, na Suécia, conforme a Figura 1. A estrutura de sustentação de cada uma dessas cabanas está representada na Figura 2. A ideia é permitir ao hóspede uma estada livre de tecnologia, mas conectada com a natureza.

A forma geométrica da superfície cujas arestas estão representadas na Figura 2 é
Resolução:
Alternativa D
Analisando a forma geométrica, é possível perceber que ela é composta por duas faces triangulares e que as demais faces são retângulos. Sendo assim, esse é um prisma quadrangular reto.
Questão 2
Analise as afirmativas a seguir e julgue-as como verdadeira ou falsa:
I – As pirâmides não são consideradas prismas.
II – Existe um prisma de base circular, também conhecido como cilindro.
III – Todo prisma possui faces laterais retangulares.
Está/Estão correta(s):
A) somente a afirmativa I.
B) somente a afirmativa II.
C) somente a afirmativa III.
D) somente as afirmativas I e III.
E) todas as afirmativas.
Resolução:
Alternativa A
I – Verdadeira
Sabemos que a pirâmide possui faces laterais triangulares e somente uma base, logo ela não é um prisma.
II – Falsa
O cilindro não pode ser considerado um prisma. Para uma forma ser um prisma, sua base deve ser um polígono. O círculo não é um polígono.
III – Falsa
Quando o prisma é oblíquo, sua face lateral é formada por paralelogramos, e não retângulos.