O volume da pirâmide é calculado pelo produto entre a área da base e a altura dividido por três. A base pode ser formada por qualquer polígono.
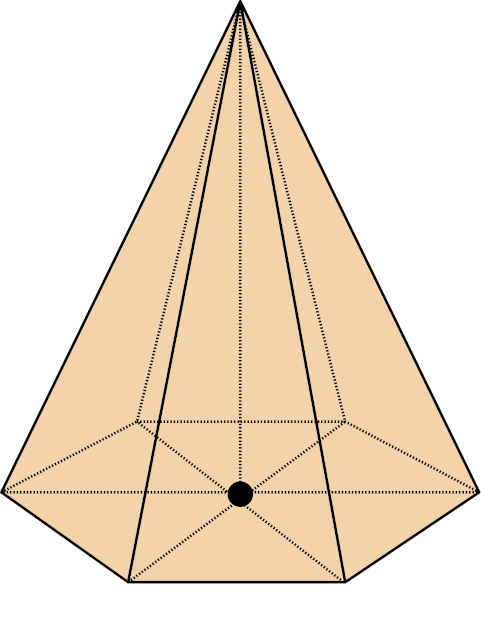
O volume da pirâmide é calculado por meio do produto entre a área da base e a altura dividido por três. A área da base da pirâmide é calculada de acordo com o polígono que forma essa base. Vale ressaltar que o volume da pirâmide é igual à terça parte do volume do prisma que possui a mesma base e a mesma altura.
A pirâmide é um sólido geométrico com faces laterais triangulares, e a base pode ser formada por polígonos, como triângulo, quadrado ou hexágono.
Leia também: Volume do cone — fórmula e exemplos de cálculo de volume desse corpo redondo
Para determinar a fórmula do volume de uma pirâmide, é necessário identificarmos dois elementos importantes: a altura e a área da base.
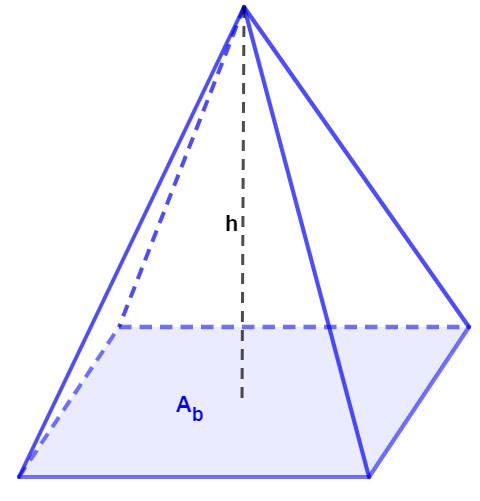
A fórmula utilizada para calcular o volume da pirâmide é o produto entre a área da base e a altura dividido por três.
\(\mathbf{V}=\frac{\mathbf{A}_\mathbf{b}\cdot\mathbf{h}}{\mathbf{3}}\)
V: volume
Ab: área da base
h: altura
Para que seja possível calcular o volume, é fundamental conhecermos o formato da base da pirâmide, pois a área da base depende do polígono. A pirâmide pode ser formada por um polígono qualquer, como um quadrado, um retângulo, um hexágono, um triângulo, entre outros.
Vamos começar pela pirâmide de base mais simples, a pirâmide de base triangular. Como o nome sugere, é a pirâmide que possui a base formada por um triângulo.
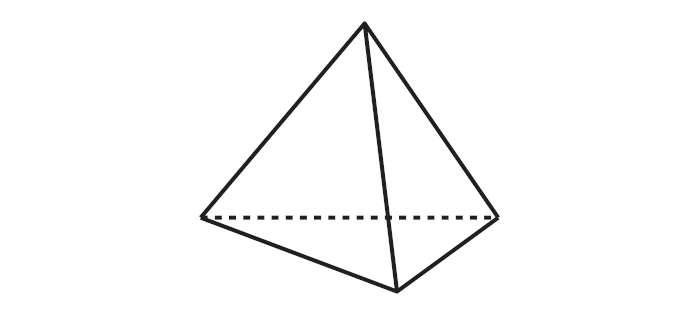
Vejamos um exemplo de cálculo do volume desse tipo de pirâmide.
Exemplo: Uma pirâmide possui base triangular. Considerando que a altura é de 20 cm, que o triângulo da base possui lado medindo 8 cm e que a altura relativa a esse lado mede 6 cm, calcule o volume da pirâmide.
Resolução:
Primeiramente, calcularemos a área da base da pirâmide. A base é um triângulo, então a área da base é:
\(A_b=\frac{b\cdot h}{2}\)
Se b = 8 e h = 6, temos que:
\(A_b=\frac{8\cdot6}{2}\)
\(A_b=\frac{48}{2}\)
\(A_b=24\ cm²\)
Conhecendo a área da base, é possível calcular o volume:
\(V=\frac{A_b\cdot h}{3}\)
A altura da pirâmide é de 20 cm, e a área da base é de 24 cm². Logo:
\(V=\frac{24\cdot20}{3}\)
\(V=\frac{480}{3}\)
\(V=160\ cm^3\)
A base dessa pirâmide é um quadrado. Sabemos que a área do quadrado é igual ao quadrado do seu lado. Para descobrir o volume dessa pirâmide, portanto, calculamos a área da base por l², sendo l o comprimento do lado da sua base, vezes a altura dividida por três.

Exemplo: Uma pirâmide possui base quadrada. Considerando que o lado dessa base mede 5 cm e que a altura é de 9 cm, qual o volume da pirâmide?
Resolução:
Calculando a área da base:
\(A_b=l^2\)
\(A_b=5^2\)
\(A_b=25\)
Agora, calculando o volume:
\(V=\frac{A_b\cdot h}{3}\)
\(V=\frac{25\cdot9}{3}\)
\(V=\frac{225}{3}\)
\(V=75\ cm^3\)
A base da pirâmide pode ser formada por hexágono também. Quando a base da pirâmide é um hexágono regular, é possível utilizar a fórmula da área da base do hexágono para calcular o volume.
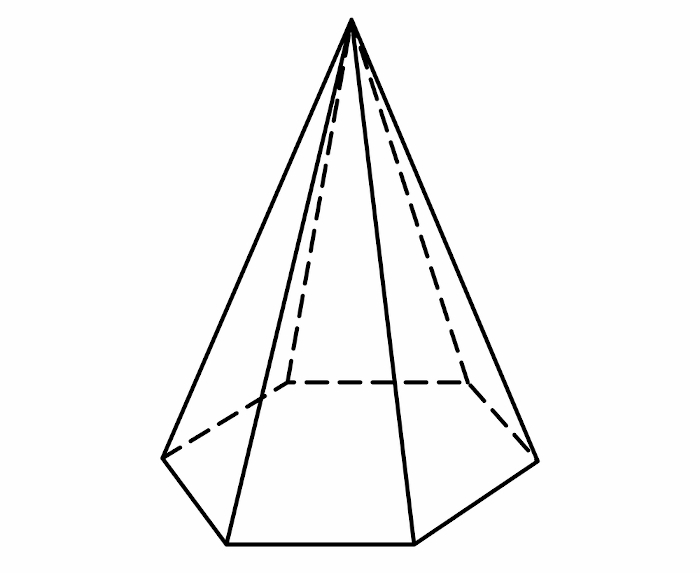
Exemplo: Uma pirâmide possui base formada por um hexágono regular com lados medindo 4 cm. Se a altura dessa pirâmide é de 8 cm, qual o seu volume?
Resolução:
A base é formada por um hexágono regular. Assim, a área da base dessa pirâmide é calculada pela fórmula:
\(A_b=\frac{3\cdot l^2\sqrt3}{2}\)
\(A_b=\frac{3\cdot4^2\sqrt3}{2}\)
\(A_b=\frac{3\cdot16\sqrt3}{2}\)
\(A_b=3\cdot8\sqrt3\)
\(A_b=24\sqrt3\)
Então, o volume será de:
\(V=\frac{A_b\cdot h}{3}\)
\(V=\frac{24\sqrt3\cdot8}{3}\)
\(V=8\sqrt3\cdot8\)
\(V=24\sqrt3\ cm^3\)
Leia também: Volume do cilindro — fórmulas e exemplos de cálculo do volume dessa figura geométrica
Comparando o volume de um prisma com o de uma pirâmide, tendo esses sólidos a mesma altura e a mesma área da base, podemos afirmar que o volume da pirâmide é igual a um terço do volume do prisma.
\(V_{prisma}=A_b\cdot h\)
\(V_{pirâmide}=\frac{A_b⋅h}3\)
Note que a fórmula da pirâmide é igual à fórmula do prisma dividida por 3.
Questão 1
Uma embalagem será confeccionada no formato de uma pirâmide com base quadrada de 5 cm de lado. Nessas condições, qual deve ser a altura da pirâmide para que o seu volume seja igual a 100 cm³?
A) 6
B) 9
C) 12
D) 15
E) 16
Resolução:
Alternativa C
Calculando o volume, temos que:
\(V=\frac{A_b\cdot h}{3}\)
Como a base é um quadrado de lados medindo 5 cm cada, a área da base \(A_b\) é 5² = 25 cm. Sabemos também que o volume V = 100, então:
\(100=\frac{25\cdot h}{3}\)
\(100\cdot3=25\cdot h\)
\(300\ =25h\)
\(h=\frac{300}{25}\)
\(h=12\ cm\)
Questão 2
Uma pirâmide possui base retangular com lados medindo 8 cm e 10 cm. Se ela possui uma altura de 15 cm, seu volume é de:
A) 250 cm³
B) 300 cm³
C) 350 cm³
D) 400 cm³
E) 450 cm³
Resolução:
Alternativa D
Como a base é um retângulo, a área da base pode ser calculada por:
\(A_b=8\cdot10=80cm^2\)
Sendo a altura de 15 cm, temos que:
\(V=\frac{A_b\cdot h}{3}\)
\(V=\frac{80\cdot15}{3}\)
\(V\ =\ 80\ \cdot5\)
\(V\ =\ 400\ cm³\)