O volume de sólidos geométricos é o espaço que cada sólido ocupa. O formato da base e a altura do sólido influenciam diretamente em seu volume.

O volume de um sólido geométrico é a medida do espaço que esse sólido ocupa. Como os sólidos geométricos possuem diferentes formatos, precisamos identificar o tipo de sólido para calcular seu volume.
Leia também: Planificação de sólidos geométricos
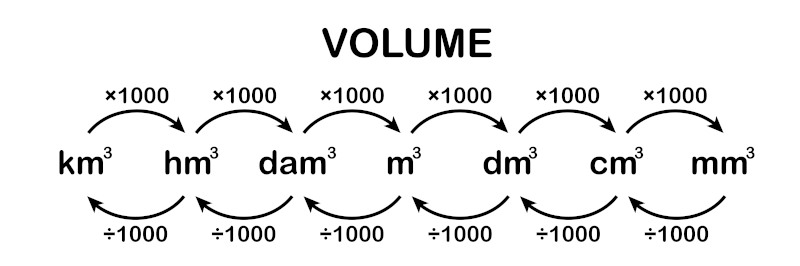
O Sistema Internacional de Unidades estabelece o metro cúbico (m³) como unidade de medida padrão de volume. Outras unidades importantes de volume são o quilômetro cúbico (km³), o centímetro cúbico (cm³) e o milímetro cúbico (mm³).
Ainda que menos comuns, também são unidades de medida de volume o hectômetro cúbico (hm³), decâmetro cúbico (dam³) e o decímetro cúbico (dm³).
Em alguns casos, é necessário converter uma unidade de medida em outra. Para isso, precisamos conhecer como as unidades se relacionam. As relações entre as principais unidades de medida de volume são:
Com exceção da esfera, cujo volume depende exclusivamente do raio, o cálculo do volume de um sólido geométrico está associado a dois elementos: a forma geométrica plana que compõe a base do sólido e a altura do sólido. Veja a seguir como é feito o cálculo do volume dos principais sólidos geométricos.

O volume de um cubo é obtido pelo produto entre a área da base e a altura. Como as faces de um cubo são formadas por quadrados congruentes, então todas as arestas têm o mesmo tamanho. Se a é a medida da aresta do cubo, então:
\(V_{cubo}=a^3\)
Qual o volume de um cubo com aresta a = 2 cm ?
Resolução:
O volume desse cubo é
\(V_{cubo}=2^3=\ 8 cm³\)
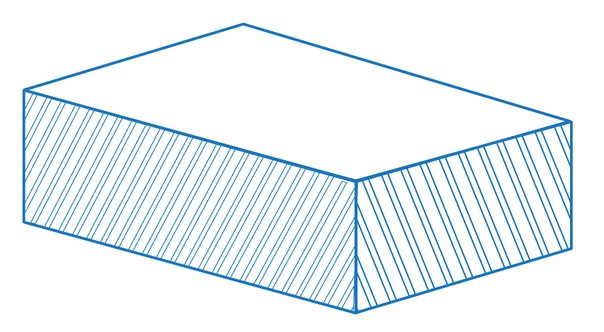
O volume de um paralelepípedo é dado pelo produto entre a área da base e a altura. Se o paralelepípedo é reto-retângulo (como uma caixa de sapatos), então o volume é obtido pelo produto entre as três dimensões (comprimento, largura e altura). Se a é a medida do comprimento do paralelepípedo reto-retângulo, b é a medida da altura e c é a medida da largura, então:
\(V_{paralelepípedo}=a.b.c\)
Qual o volume de um paralelepípedo com 3 cm de comprimento, 7 cm de altura e 2 cm de largura?
Resolução:
O volume desse paralelepípedo é
\(V_{paralelepípedo}=3.7.2 = 42 cm³\)
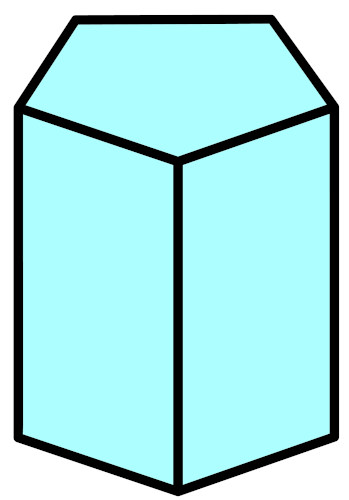
O volume de um prisma é obtido pelo produto entre a área da base e a altura. Lembre-se que a base de um prisma é uma forma geométrica plana. Se Ab é a área da base do prisma e h é a altura do prisma, então:
\(V_{prisma}=A_b.h\)
Determine o volume de um prisma triangular regular sabendo que sua altura é 8 cm e que o lado do triângulo equilátero que forma a base é 1 cm.
Resolução:
Primeiro precisamos descobrir a área da base triangular. Lembre-se que a área de um triângulo equilátero é \(\frac{l\sqrt3}{2}\) . Assim,
\(A_b=\frac{1\ .\ \sqrt3}{2}\ =\ \frac{\sqrt3}{2} cm²\)
Portanto, o volume do prisma é:
\(V_{prisma}=\frac{\sqrt3}{2}.8=4\sqrt3 cm³\)
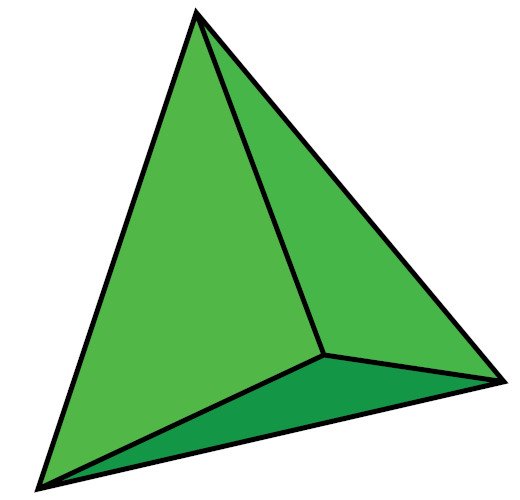
O volume de uma pirâmide corresponde a um terço do produto entre a área da base e a altura. Lembre-se de que a base de uma pirâmide é uma forma geométrica plana.
\(V_{pirâmide}=\frac{1}{3}A_b.h\)
Uma pirâmide de base quadrada possui 10 cm de altura e 3 cm de aresta da base. Determine seu volume.
Resolução:
Primeiro precisamos encontrar a área da base quadrada:
\(A_b=3.3=9 cm²\)
Portanto, o volume da pirâmide é
\(V_{pirâmide}=\frac{1}{3}9.10=30cm³\)

O volume de um cilindro é obtido pelo produto entre a área da base e a altura. Como a base de um cilindro é um círculo, cuja área é dada por πr2 (em que r é o raio do círculo), a expressão do volume do cilindro é:
\(V_{cilindro}=A_b.h=\pi r^2h\)
Calcule o volume de um cilindro de 6 cm de altura cujo raio da base mede 4 cm.
Resolução:
O volume desse cilindro é
\(V_{cilindro}=\pi4^26=\ 96\pi cm³\)

O volume de um cone corresponde a um terço do produto entre a área da base (que é a área de um círculo de raio r ) e a altura.
\(V_{cone}=\frac{1}{3}A_b.h=\frac{1}{3}\pi r^2.h\)
Qual o volume de um cone com 12 cm de altura e 3 cm de raio da base?
Resolução:
O volume desse cone é:
\(V_{cone}=\frac{1}{3}\pi3^2.12\ =36 cm³\)

O volume de uma esfera corresponde a quatro terços do produto entre π e r3 , sendo r o raio da esfera.
\(V_{esfera}=\frac{4}{3}\pi r^3\)
Qual o volume de uma esfera com 2 cm de raio?
Resolução:
O volume dessa esfera é:
\(V_{esfera}=\frac{4}{3}\pi2^3=\frac{32}{3}\pi cm³\)
Veja também: Diferença entre circunferência, círculo e esfera
Os conceitos de volume e capacidade são semelhantes, mas não são iguais. Enquanto o volume é o espaço ocupado por um corpo (como um sólido geométrico), capacidade é o espaço disponível no interior de um objeto. Em outras palavras, a capacidade é o volume interno de um recipiente. Isso significa que a capacidade não leva em consideração a espessura do recipiente.
Apesar dos conceitos distintos, as unidades de medida de volume e capacidade se relacionam. As unidades de medida de capacidade que mais utilizamos são o litro (L) e o mililitro (mL), estecorresponde a um milésimo do litro. Essas unidades aparecem, por exemplo, em embalagens de garrafas de água, leite, sucos, chás, refrigerantes e outras bebidas. Também é comum o uso do mililitro em remédios e do litro na capacidade de tanques de gasolina. 1 metro cúbico vale 1000 litros e, consequentemente, 1 centímetro cúbico vale 1 mililitro.
Questão 1
Um cubo possui 64 m³ de volume. Se a é a aresta desse cubo, então:
A) a = 1 m
B) a = 2 m
C) a = 3 m
D) a = 4 m
E) a = 5 m
Resolução:
Alternativa D.
O volume de um cubo é dado por a3 , em que a é a medida da aresta. Assim,
\(V_{cubo}=a^3\)
\(64=a^3\)
\(a\ =\ 4 cm\)
Questão 2
Pedro estava estudando dois sólidos geométricos:
I. Pirâmide de base quadrada com altura 3 cm e lado da base 4 cm.
II. Esfera com 5 cm de raio.
Utilizando a aproximação π = 3 , determine qual dos sólidos possui maior volume.
Resolução:
Primeiro vamos calcular o volume da pirâmide. Como a base da pirâmide é um quadrado de lado com 4 cm, a área da base da pirâmide mede 16 cm². Assim,
\(V_{esfera}=\frac{1}{3}.{16.3}=16 cm³\)
Agora vamos calcular o volume da esfera.
Como o raio r da esfera mede 1 cm e devemos utilizar a aproximação π = 3 , concluímos que:
\(V_{esfera}=\frac{4}{3}.{3.1}^3=4 cm³\)
Portanto, nesse caso, a pirâmide é o sólido com maior volume.