O paralelepípedo é um sólido geométrico que possui todas as faces com paralelogramos. Essa forma pode ser percebida nos prédios e em caixas de sapatos.

O paralelepípedo é um sólido geométrico que possui três dimensões: altura, largura e comprimento. Esse prisma possui todas as suas faces no formato de um paralelogramo, sendo formado por 6 faces, 8 vértices e 12 arestas. É uma forma geométrica bastante comum no nosso cotidiano, observada, por exemplo, em caixas de sapato, no formato de algumas piscinas etc. O volume de um paralelepípedo é calculado pelo produto do comprimento de suas três dimensões. Já a sua área total é igual à soma das áreas das suas faces.
Leia também: Planificação de sólidos geométricos — a representação das suas faces em forma bidimensional
O paralelepípedo é um sólido geométrico formado por faces no formato de paralelogramos.
É composto por 6 faces, 8 vértices e 12 arestas.
Ele pode ser oblíquo ou reto.
Para calcular o volume de um paralelepípedo, calculamos o produto entre a altura, largura e comprimento do paralelepípedo.
A área total de um paralelepípedo é calculada por AT = 2ab + 2ac + 2bc.
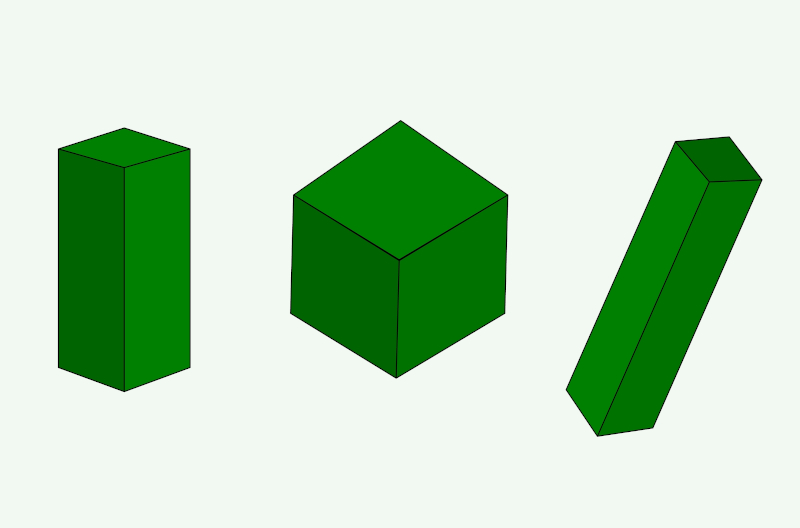
O paralelepípedo é um sólido geométrico que possui as faces formadas por paralelogramos. Esse formato é bastante comum no nosso cotidiano, sendo um caso particular de prisma, pois os prismas são sólidos geométricos que possuem duas bases congruentes. Para se caracterizarem como paralelepípedos, portanto, as bases são formadas por paralelogramos. Sendo assim, o paralelepípedo possui 6 faces formadas por paralelogramos, 8 vértices e 12 arestas. Veja abaixo:
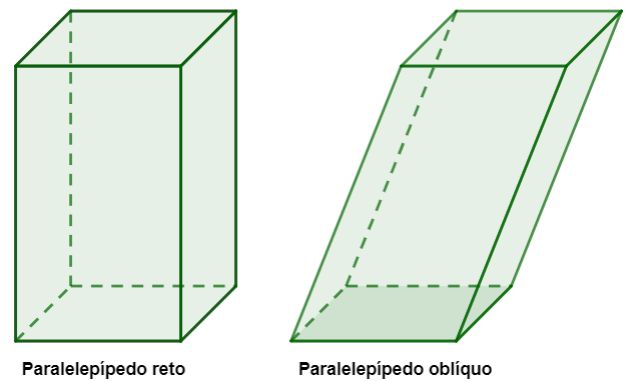
Existem duas classificações possíveis para um paralelepípedo:
Paralelepípedo reto: quando as arestas das faces laterais são perpendiculares à base.
Paralelepípedo oblíquo: quando as arestas laterais são oblíquas à base.
Existem fórmulas específicas para calcular o volume, a área total e o comprimento da diagonal de um paralelepípedo reto. O paralelepípedo oblíquo não possui fórmulas específicas para esses cálculos, já que ele depende, principalmente:
da forma da sua base;
da sua inclinação.
Além desses, ele depende de vários outros fatores que são estudados mais a fundo no Ensino Superior. No nosso cotidiano, o mais recorrente é o paralelepípedo reto, conhecido também como paralelepípedo retângulo. Veja, a seguir, como calcular o seu volume, sua área e sua diagonal.
Para calcular o volume de um paralelepípedo, basta que seja feita a multiplicação do comprimento, da largura e da altura desse sólido geométrico.
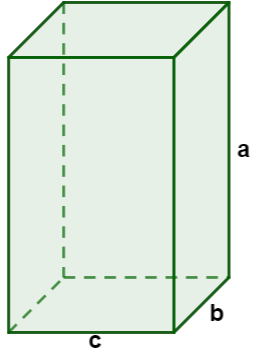
Para calcular o volume do paralelepípedo, utilizamos a seguinte fórmula:
\(V=a\cdot b\cdot c\)
Uma caixa possui formato de um paralelepípedo reto, com 10 cm de altura, 6 cm de largura e 8 cm de largura. Qual é o volume dessa caixa?
Resolução:
Para calcular o volume, multiplicaremos as três dimensões dadas, ou seja:
\(V=a\cdot b\cdot c\)
\(V=10\cdot6\cdot8\)
\(V=60\cdot8\)
\(V=480\ cm^3\)
Portanto, o volume dessa caixa é de 480 cm³.
Saiba mais: Medidas de volume — quais são elas?
A área de um sólido geométrico é a soma das áreas das suas faces. Um paralelepípedo é composto por 6 faces. Ademais, analisando esse sólido, é possível perceber que as faces opostas são congruentes. Em um paralelepípedo reto, as faces são formadas por retângulos. Assim, para calcular a área de cada uma das faces, basta multiplicar as duas dimensões da face.
Já para calcular a área total do paralelepípedo, utilizamos a seguinte fórmula:
\(A_T=2ab+2ac+2bc\)
Calcule a área total do paralelepípedo a seguir:
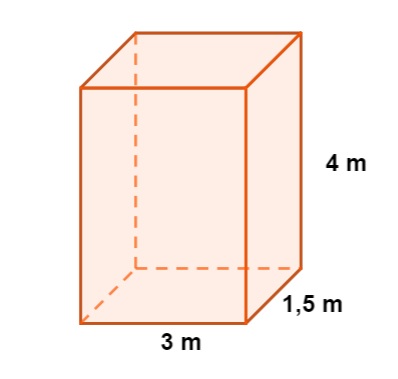
Resolução:
Calculando a área total, temos que:
\(A_T=2\cdot4\cdot1,5+2\cdot4\cdot3+2\cdot3\cdot1,5\)
\(A_T=12+24+9\)
\(A_T=45m^2\)
Então, a área total desse paralelepípedo é de 45 m².
Quando traçamos a diagonal de um paralelepípedo, é possível também calcular o seu comprimento. Para isso, é preciso conhecer a medida desse sólido geométrico.
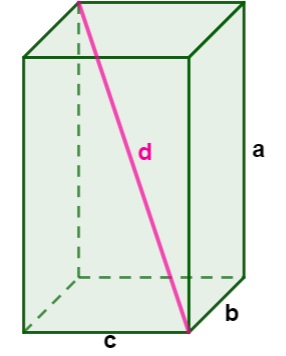
Para calcular o comprimento da diagonal do paralelepípedo, utilizamos a seguinte fórmula:
\(d=\sqrt{a^2+b^2+c^2}\)
Qual é o comprimento da diagonal de um paralelepípedo que possui altura igual a 6 cm, largura igual a 6 cm e comprimento igual a 7 cm?
Resolução:
Calculando o comprimento da diagonal, temos que:
\(d=\sqrt{6^2+6^2+7^2}\)
\(d=\sqrt{36+36+49}\)
\(d=\sqrt{121}\)
\(d=11 cm\)
Saiba também: Diagonais de um polígono — como calcular sua quantidade?
Questão 1
(Técnico integrado - IFG) As medidas internas de um reservatório no formato de um paralelepípedo são de 2,5 m de comprimento, 1,8 m de largura e 1,2 m de profundidade (altura). Se, em determinado momento do dia, esse reservatório está apenas com 70% de sua capacidade, a quantidade de litros que faltam para enchê-lo é igual a:
A)1620
B)1630
C)1640
D)1650
E) 1660
Resolução:
Alternativa A
Para calcular o volume, multiplicaremos as dimensões:
\(V=\mathrm{2,5}⋅1{,8}\cdot\mathrm{1,2}\)
\(V=\mathrm{5,4}m\)
Para transformar a capacidade de 5,4 m³ para litros, é necessário fazer a conversão da unidade de medida de capacidade, multiplicando por 1000, ou seja:
V = 5,4 · 1000 = 5400 litros
Sabemos que 70% do reservatório está cheio, restando 30% dessa capacidade para terminar de enchê-lo. Logo, a quantidade que falta é de:
30% de 5400 = 0,3 · 5400 = 1620 litros
Questão 2
Um bloco retangular possui diagonal medindo 12,5 cm, altura igual a 7,5 cm e largura de 8 cm. A medida do comprimento desse bloco é de:
A) 5 cm
B) 6 cm
C) 7 cm
D) 9 cm
E) 10 cm
Resolução:
Alternativa B
Utilizando a fórmula da diagonal, temos que:
\(d=\sqrt{a^2+b^2+c^2}\)
\(\mathrm{12,5}=\sqrt{{\mathrm{7,5}}^2+8^2+c^2}\)
\({\mathrm{12,5}}^2=\sqrt{{\mathrm{56,25}+64+c^2}^2}\)
\(\mathrm{156,25}=\mathrm{56,25}+64+c^2\)
\(\mathrm{156,25}-\mathrm{56,25}-64=c^2\)
\(100-64=c^2\)
\(36=c^2\)
\(c=\sqrt{36}\)
\(c=6 cm\)