A Geometria Plana é a área da Geometria que analisa figuras bidimensionais, com o estudo de elementos importantes, como o ponto, a reta, o plano e as figuras planas.
A Geometria Plana está presente a todo instante no nosso cotidiano. Quando observamos o mundo à nossa volta, é possível notar várias formas geométricas. Quando as formas geométricas possuem duas dimensões, elas são objeto de estudo da Geometria Plana.
O ponto, a reta e o plano são elementos primitivos estudados na Geometria Plana, além das noções de ângulos e do estudo das figuras planas, como o quadrado, o triângulo, o retângulo, o trapézio, o círculo e o losango. Além da geometria plana, existe também a Geometria Espacial, uma outra área da Matemática, que estuda as figuras geométricas tridimensionais. O estudo da Geometria Plana é essencial para compreender o espaço em que vivemos.
Saiba mais: Geometria Analítica — área que estuda a Geometria utilizando ferramentas algébricas
A Geometria Plana é a área da Matemática que estuda as figuras planas.
Ponto, reta e plano são os conceitos primitivos dessa Geometria.
Existem conceitos importantes que são a base da Geometria Plana e que são desenvolvidos a partir dos conceitos primitivos.
Muitas figuras planas são estudadas na geometria plana, como o triângulo, o paralelogramo, o retângulo, o losango, o quadrado, o trapézio, a circunferência e o círculo.
Existem fórmulas importantes para o cálculo das medidas de cada uma das figuras planas, como o perímetro, que é a soma do contorno da figura, e o cálculo da área:
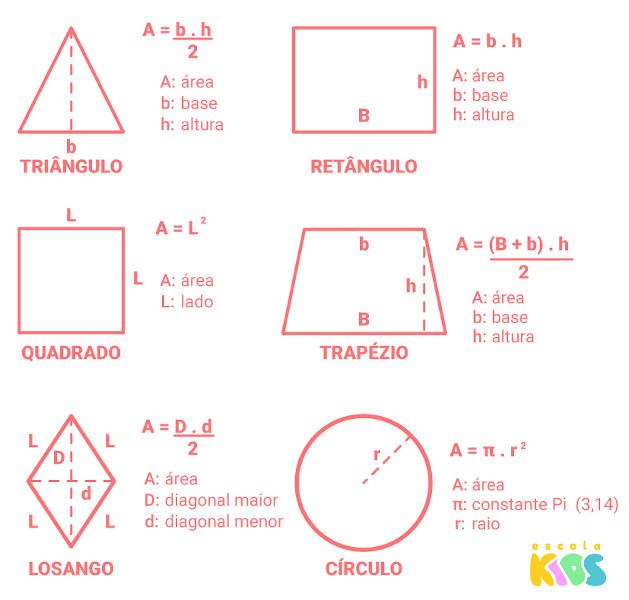
No estudo da Geometria Plana, foram desenvolvidos conceitos importantes, começando pelos conceitos primitivos, que são os de ponto, reta e plano. Esses objetos são conhecidos como primitivos por serem base para o desenvolvimento de outros conceitos, como os de ângulo, semirreta, segmento de reta, polígono, área etc. Vejamos cada um deles.
O ponto, a reta e o plano são elementos primitivos da Matemática, ou seja, não possuem definição, mas são objetos que estão em nossa imaginação, compreendidos de maneira intuitiva, e são essenciais para a construção dos conceitos da Geometria Plana.
O ponto é o objeto mais simples da Geometria. Ele não possui dimensão, ou seja, é adimensional, e nos auxilia a encontrar a localizações no plano de forma precisa. O seu uso é comum para representar uma localização em GPS de aplicativos, por exemplo.
A reta, por sua vez, é formada por um conjunto de pontos que estão alinhados. Em um plano, há pontos que estão na reta e fora da reta. Ela possui apenas uma dimensão, com largura e profundidade desprezíveis. As retas são infinitas e podem ser a representação de uma trajetória no plano.
O plano é uma superfície que não possui curvas, isto é, é uma região bidimensional. O plano é infinito para as duas dimensões, e nele podemos inserir infinitas retas. Quando imaginamos uma reta, sabemos que ela está contida em determinada superfície, que é o plano.
Para representar e nomear esses elementos primitivos, utilizamos as seguintes notações:
O ponto é representado por uma letra maiúscula do nosso alfabeto, como A, B, C.
A reta é representada por letra minúscula do alfabeto, como r, s, t.
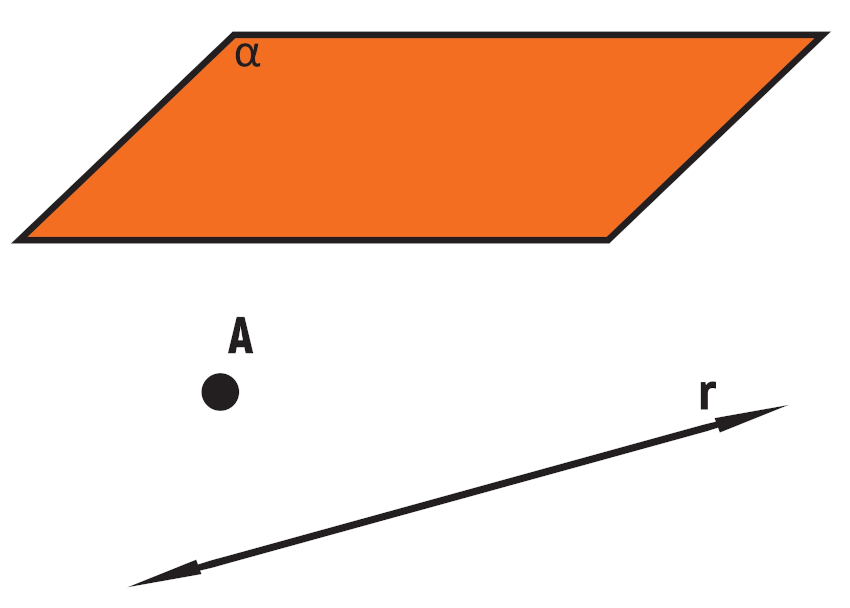
O plano é representado por uma letra grega do alfabeto, como α, β.
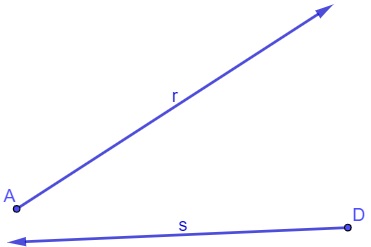
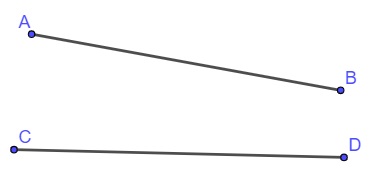
Com base nesses conceitos básicos, é possível compreender conceitos importantes, como o de semirreta e de segmento de reta. Semirreta é a parte de uma reta que possui início, porém não possui final. Para representar uma semirreta, utilizamos dois pontos — o primeiro é o ponto inicial da semirreta e o segundo é um ponto qualquer pertencente a ela. Com uma seta indicativa em cima das duas letras que representam pontos, demonstra-se que uma semirreta começa no ponto A e passa pelo ponto B: .
Adicionalmente, há o segmento de reta, que também é parte de uma reta, mas possui início e final determinados. O segmento de reta geralmente é representado pelas letras dos pontos que o limitam com um traço em cima. Por exemplo, .
Entendendo bem os conceitos envolvendo reta, semirreta e segmento de reta, é possível compreender a ideia de ângulo. A região que se encontra entre as retas será conhecida como ângulo sempre que houver o encontro de duas retas em um ponto chamado vértice.
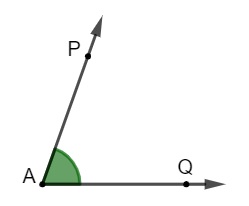
De acordo com a medida dos ângulos, é possível classificá-los como:
Ângulo agudo: se a medida for menor que 90°;
Ângulo reto: se a medida for igual a 90°;
Ângulo obtuso: se a medida for maior que 90° e menor que 180°;
Ângulo raso: se a medida for igual a 180°.
Leia também: Ângulos complementares e suplementares — o que cada um deles significa?
As figuras planas são as figuras geométricas representadas em um plano. Algumas das figuras planas foram estudadas a fundo, gerando conceitos importantes, como o de área e o de perímetro. Além disso, cada uma das figuras tem suas características estudadas.
Em relação a uma figura plana, a área é a medida da sua superfície e o perímetro é o comprimento do contorno da figura, ou seja, a soma do comprimento dos seus lados. Veja, a seguir, as principais figuras planas e as fórmulas para o cálculo de sua área e perímetro.
Conhecemos como triângulo a figura plana que possui três lados. Para descobrir o valor da sua área, calculamos o produto entre o comprimento da base, o comprimento da altura e dividimos por 2. Já o seu perímetro é encontrado por meio da soma dos lados.

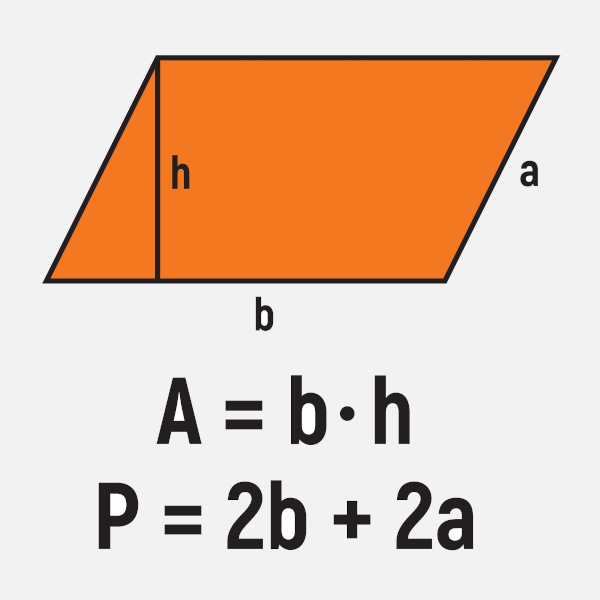
Conhecemos como paralelogramo a figura plana que possui quatro lados paralelos de dois em dois. Para descobrir o valor da área de um paralelogramo, basta calcular o produto entre sua base e altura. Já o seu perímetro é encontrado por meio da soma de todos os lados. Como os lados paralelos são congruentes, a fórmula para calcular o perímetro do paralelogramo é a soma da base com o lado oblíquo multiplicados por 2.
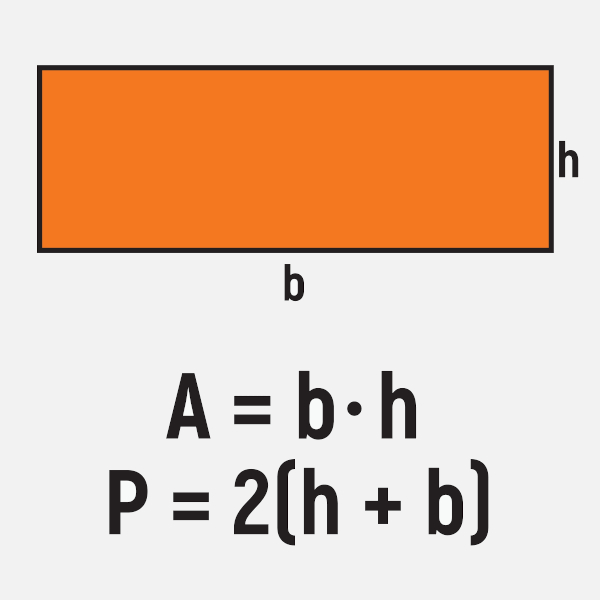
O retângulo é uma figura plana de quatro lados que possui todos os ângulos retos. Para calcular a área de um retângulo, multiplicamos a base pela altura. O valor do perímetro é igual à soma dos seus lados. Como essa figura possui lados congruentes de dois em dois, há uma fórmula para calcular o seu perímetro, que é a soma do lado maior com o lado maior multiplicada por 2.
Saiba também: Poliedro — todo sólido geométrico que possui suas faces formadas por polígonos
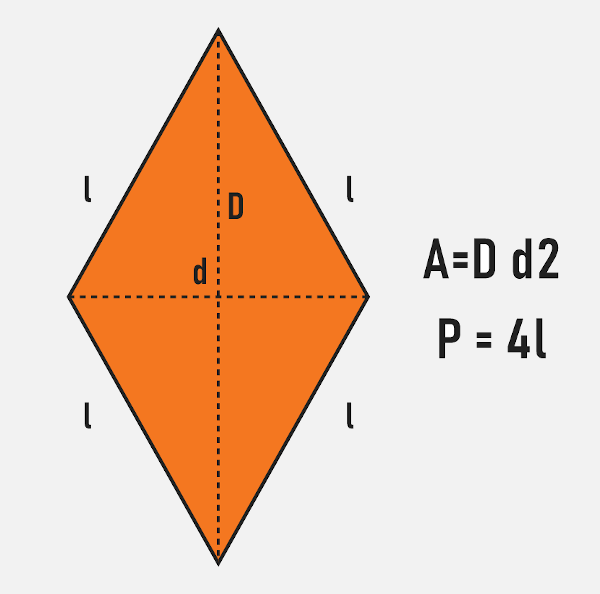
O losango é uma figura plana que, diferentemente das anteriores, possui quatro lados congruentes. Para calcular sua área é necessário encontrar o comprimento das suas diagonais, sendo que D representa a diagonal maior e d, a diagonal menor. Como possui todos os lados congruentes, para calcular o perímetro do losango basta multiplicar a medida do lado por 4.
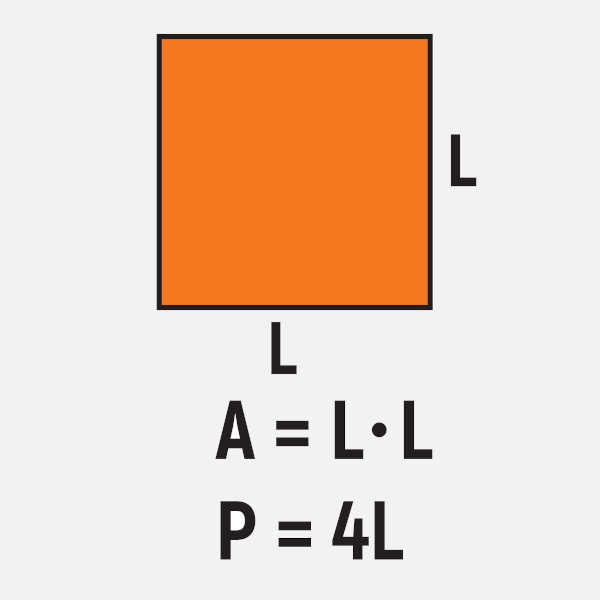
O quadrado é um caso especial de losango e retângulo, pois ele possui todos os 4 lados congruentes e também possui todos os ângulos congruentes. Para calcular a sua área, basta multiplicar a sua base pela altura. Como os lados são congruentes, basta calcular o quadrado do lado. Assim, essa figura, assim como o trapézio, possui todos os lados congruentes. Logo, o seu perímetro é calculado quando multiplicamos o comprimento do lado por 4.
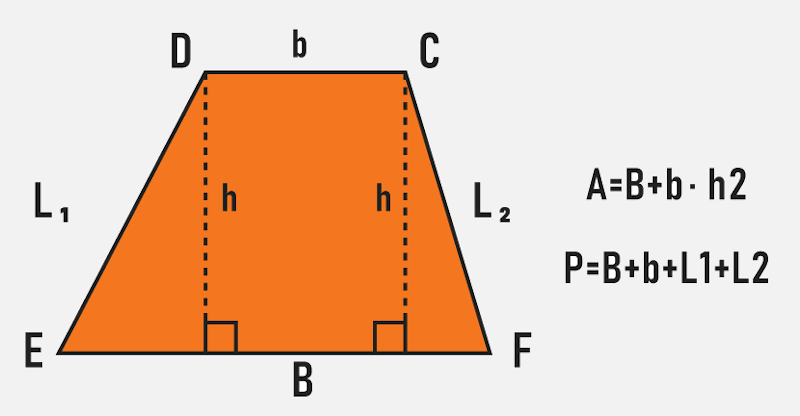
O trapézio é um quadrilátero que possui dois lados paralelos e os outros dois lados não paralelos. Para calcular a sua área, é necessário conhecer o comprimento da base maior, da base menor e da altura. Para descobrir o seu perímetro, não há fórmula específica, sendo este calculado pela soma das suas bases com os lados oblíquos.
A circunferência é a figura formada pelo conjunto de pontos que estão a uma mesma distância (r) de um ponto conhecido como centro.
O círculo é a região delimitada pela circunferência.
Para calcular a área e o comprimento do círculo, utilizamos as fórmulas as seguir:

Como vimos, a Geometria Plana é o estudo das figuras e objetos geométricos no plano. Ela se restringe, então, a duas dimensões. Nela, são estudadas figuras planas, como o quadrado, o retângulo e o triângulo. Já a Geometria Espacial estuda elementos em um universo tridimensional. Logo, nela estudamos os sólidos geométricos, que são o cubo, as pirâmides, a esfera, entre outros. A Geometria Plana é a base para o estudo da Geometria Espacial.
Acesse também: Diferença entre circunferência, círculo e esfera — dicas para nunca mais errar
Questão 1
Um campo de futebol possui 70 metros de largura e 110 metros de comprimento. Se durante o aquecimento um atleta completa 10 voltas nesse campo, ele andará um total de:
A) 180 metros
B) 360 metros
C)1800 metros
D) 3600 metros
E) 7200 metros
Resolução:
Alternativa D
Primeiramente, calcularemos o perímetro desse terreno:
P = 2 (70 + 110)
P = 2 · 180
P = 360
Como ele completou 10 voltas, então:
360 · 10 = 3600 metros
Questão 2
Uma praça possui formato circular, com raio de 8 metros. Utilizando π = 3, a área dessa praça é de:
A) 158 m²
B) 163 m²
C) 192 m²
D) 210 m²
E) 250 m²
Resolução:
Alternativa C
Calculando a área, temos:
A = πr²
A = 3 · 8²
A = 3 · 64
A = 192 m²