O losango é uma figura geométrica estudada na Geometria Plana composto por quatro lados, todos congruentes entre si. Trata-se de um caso particular de quadrilátero.

O losango é um polígono estudado na Geometria Plana. Ele é um quadrilátero que possui os quatro lados congruentes, ou seja, com a mesma medida. Assim como os demais polígonos, o losango é composto por vértices, ângulos e lados.
Para calcular a área do losango, basta encontra o valor da metade do produto entre o comprimento da diagonal maior e o comprimento da diagonal menor. O perímetro do losango é a soma dos seus 4 lados. Existe uma relação pitagórica entre o comprimento das diagonais do losango e o comprimento do seu lado.
Leia também: Quadrado — figura geométrica com quatro lados de mesma medida
\(A=\frac{D\cdot d}{2}\)
\(\left(\frac{D}{2}\right)^2+\left(\frac{d}{2}\right)^2=l^2\)
Uma figura plana é classificada como losango quando ela é um polígono que possui os quatro lados congruentes. O losango é um tipo de quadrilátero comum no nosso dia a dia, presente inclusive na bandeira nacional, na cor amarela. Veja, a seguir, uma representação de losango:
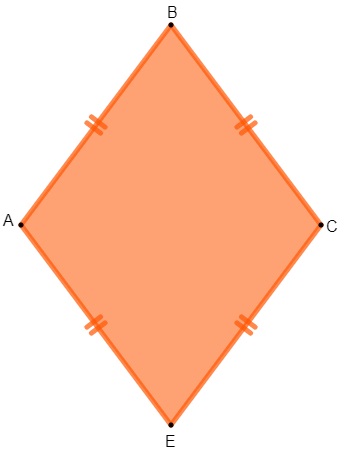
Assim como nos demais polígonos, os principais elementos do losango são os seus lados, ângulos internos, vértices e diagonais.
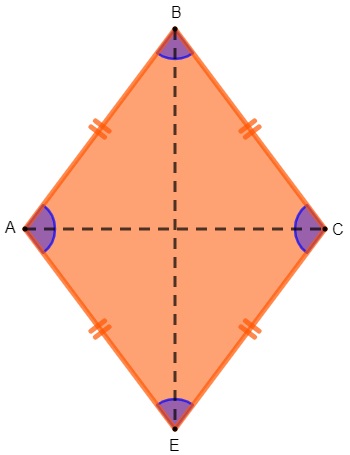
Como o losango é um quadrilátero e um paralelogramo, ele possui propriedades importantes.
Leia também: Triângulo — as propriedades da figura geométrica que possui três lados
Para calcular a área do losango, é necessário utilizar o comprimento da diagonal maior e o comprimento da diagonal menor.
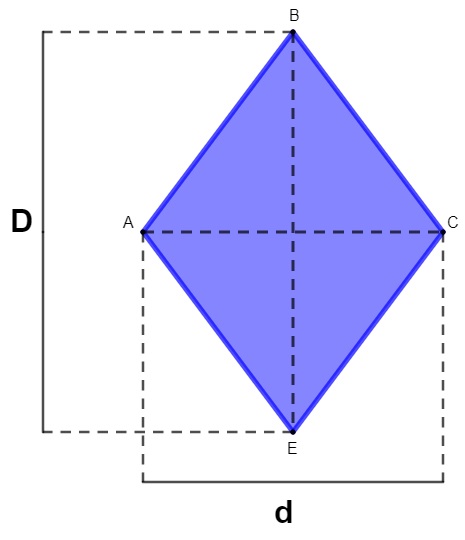
Conhecendo o comprimento das diagonais do losango, sua área pode ser calculada por:
\(A=\frac{D\cdot d}{2}\)
Exemplo:
Um losango possui diagonais medindo 12 cm e 9 cm, então qual é a sua área?
Resolução:
Sabemos que:
Substituindo os valores conhecidos na fórmula:
\(A=\frac{D\cdot d}{2}\)
\(A=\frac{12\cdot9}{2}\)
\(A=\frac{96}{2}\)
\(A=54cm^2\)
O perímetro do losango é igual à soma dos seus lados. Como todos os lados do losango possuem a mesma medida, para calcular seu perímetro, basta multiplicar o comprimento do lado por 4:
\(P=4l\ \)
Exemplo:
Qual é o perímetro de um losango, sabendo que um dos seus lados mede 8 cm?
Resolução:
Se um lado mede 8 cm, todos os lados medem 8 cm. Assim, o perímetro desse losango é:
\(P=4l\)
\(P=4\cdot8\)
\(P=32\ cm\ \)
Como as diagonais se cruzam de forma perpendicular e no ponto médio da diagonal, é possível termos uma relação pitagórica entre o lado e as diagonais do losango:
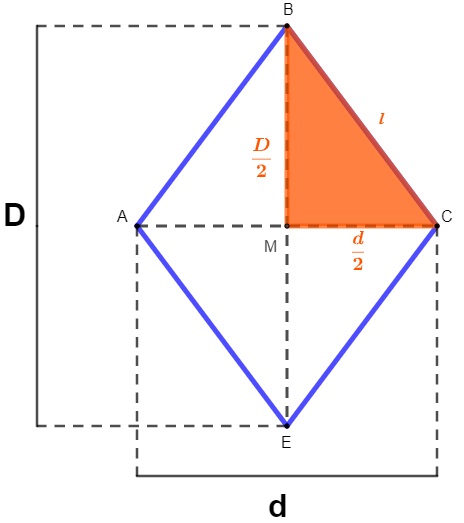
No triângulo BMC, há uma relação pitagórica entre os lados e a metade da medida das diagonais do losango, pois temos que:
\(l^2=\left(\frac{D}{2}\right)^2+\left(\frac{d}{2}\right)^2\)
Leia também: Fórmulas e como calcular a área das principais figuras planas
Questão 1
Um losango possui diagonais medindo 16 cm e 12 cm, então seu perímetro é igual a:
A) 16 cm
B) 32 cm
C) 38 cm
D) 40 cm
Resolução:
Alternativa D
Sabemos que:
Para encontrar o comprimento do lado do losango, utilizaremos o teorema de Pitágoras:
\(l^2=\left(\frac{16}{2}\right)^2+\left(\frac{12}{2}\right)^2\)
\(l^2=8^2+6^2\)
\(l^2=64+36\)
\(l^2=100\)
\(l=\sqrt{100}\)
\(l\ =\ 10\ \)
Sabendo que o lado mede 10 cm, o perímetro desse losango é igual a:
\(P=4l\ \)
\(P=4\cdot10\)
\(P=40\ cm\)
Questão 2
Um terreno possui formato de losango com a diagonal maior medindo 18 metros e a diagonal menor medindo 10 metros. A área desse terreno é de:
A) 100 m²
B) 90 m²
C) 80 m²
D) 70 m²
E) 60 m²
Resolução:
Alternativa B
Calculando a área do terreno, temos:
\(A=\frac{D\cdot d}{2}\)
\(A=\frac{18\cdot10}{2}\)
\(A=\frac{180}{2}\)
\(A=90m^2\)