Cilindro é um sólido geométrico estudado na geometria espacial que é bastante comum no dia a dia. É composto por duas bases circulares e sua área lateral.

O cilindro é um sólido geométrico bastante comum no cotidiano, pois é possível identificar vários objetos que têm o formato dele, como um lápis, determinadas embalagens, cilindros de oxigênio, entre outros. Existem dois tipos de cilindro: o cilindro reto e o cilindro oblíquo.
O cilindro é formado por duas bases circulares e área lateral. Por ter uma base circular, ele é classificado como um corpo redondo. Para calcular a área da base, a área lateral, a área total e o volume do cilindro, utilizamos fórmulas específicas. A planificação do cilindro é composta por dois círculos, que são as suas bases, e um retângulo, que é a sua área lateral.
Veja também: Cone — o que é, elementos, classificação, área, volume
\(A_b=\pi r^2\)
\(A_l=2\pi rh\)
\(A_T=2\pi r^2+2\pi rh\)
\(V=\pi r^2\cdot h\)
O cilindro é um sólido geométrico que tem duas bases e uma área lateral. Suas bases são formadas por dois círculos, o que colabora para o fato de que o cilindro é um corpo redondo. Seus principais elementos são as duas bases, a altura, a área lateral e o raio da base. Veja a seguir:
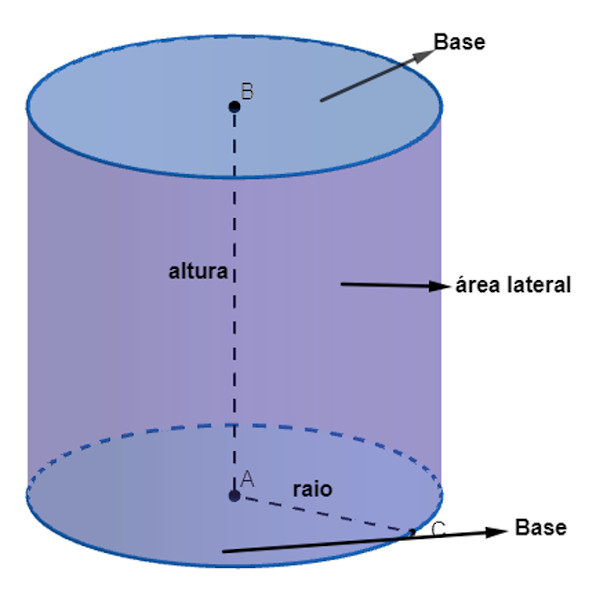
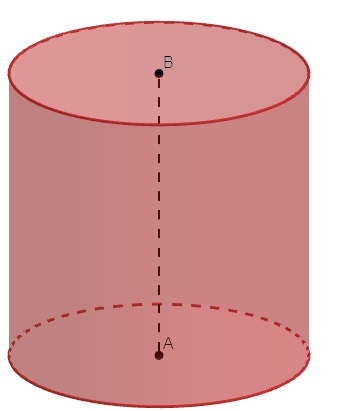
Existem dois tipos de cilindro: o reto e o oblíquo.
Quando o eixo é perpendicular às bases.
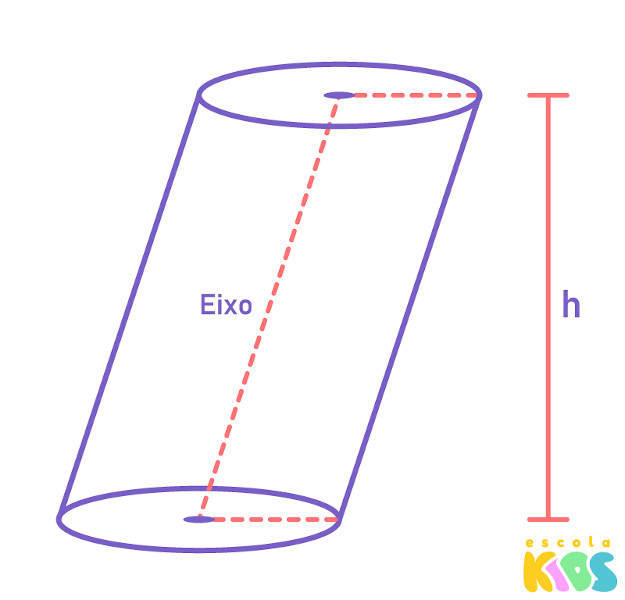
Quando ele é inclinado.
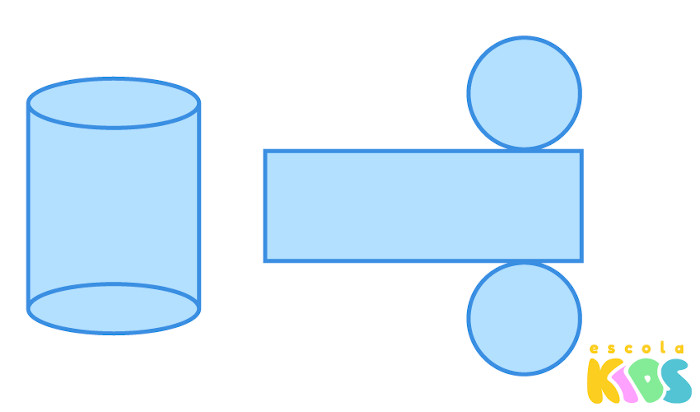
A planificação de sólidos geométricos é a representação de suas faces de forma plana. O cilindro é composto por duas bases que têm formato de um círculo, e a sua área lateral é um retângulo, como mostra a figura:
Existem cálculos importantes envolvendo cilindro, são eles: área da base, área lateral, área total e área do volume. Cada um deles possui fórmula específica.
Como sabemos, a base de um cilindro é formada por um círculo, sendo assim, para calcular a sua área da base, utilizamos a fórmula da área de um círculo:
\(A_b=\pi r^2\)
Calcule a área da base de um cilindro que possui raio medindo 8 cm.
(Utilize \(π=3,14\))
Resolução:
Calculando a área da base, temos que:
\(A_b=\pi r^2\)
\(A_b=3,14\cdot8^2\)
\(A_b=3,14\cdot64\)
\(A_b=200,96\ cm^2\)
Leia também: Como calcular a área do triângulo?
A área lateral do cilindro é um retângulo, mas sabemos que ele contorna o círculo da base, então um dos seus lados mede o mesmo que o comprimento da circunferência, logo, sua área é igual ao produto entre o comprimento da circunferência da base e a altura. A fórmula para se calcular a área lateral é:
\(A_l=2\pi r\cdot h\)
Calcule a área lateral de um cilindro cuja altura é de 6 cm, o raio é de 2 cm, e π=3,1.
Resolução:
Calculando a área lateral, temos que:
\(A_l=2\cdot3,1\cdot2\cdot6\)
\(A_l=6,1\cdot12\)
\(A_l=73,2\ cm²\)
A área total de um cilindro nada mais é que a soma da área das suas duas bases com a área lateral:
\(A_T=A_l+2A_b\)
Então temos que:
\(A_T=2\pi rh+2\pi r^2\)
Calcule a área total de um cilindro que possui r = 8 cm, altura igual a 10 cm, e utilizando \(π=3\).
Resolução:
\(A_T=2\cdot3\cdot8\cdot10+2\cdot3\cdot8^2\)
\(A_T=380+6\cdot64\)
\(A_T=380+384\)
\(A_T=764\)
O volume é uma grandeza muito importante para os sólidos geométricos, e o volume do cilindro é igual ao produto entre a área da base e a altura, sendo assim, o volume é dado por:
\(V=\pi r^2\cdot h\)
Qual é o volume de um cilindro que tem raio igual a 5 cm e altura igual a 12 cm? (Use \(π=3\))
Resolução:
Calculando o volume do cilindro, temos que:
\(V=3\cdot5^2\cdot12\)
\(V=\ 3\ \cdot25\ \cdot12\)
\(V=900\ cm^3\ \)
Questão 1
A embalagem de determinado produto tem a base de 10 cm de diâmetro e a altura de 18 cm. Então o volume dessa embalagem e de:
(Use \(π = 3\))
A) 875 cm³
B) 950 cm³
C) 1210 cm³
D) 1350 cm³
E) 1500 cm³
Resolução:
Alternativa D
Sabemos que o raio é igual à metade do diâmetro, então:
r = 10 : 2 = 5 cm
Calculando o volume, temos que:
\(V=\pi r^2\cdot h\)
\(V=3\cdot5^2\cdot18\)
\(V=\ 3\cdot25\cdot18\)
\(V=\ 75\cdot18\ \)
\(V=1350\ cm³\)
Questão 2
(USF-SP) Um cilindro circular reto, de volume 20π cm³, tem altura de 5 cm. Sua área lateral, em centímetros quadrados, é igual a:
A) 10π
B) 12π
C) 15π
D) 18π
E) 20π
Resolução:
Alternativa E
Sabemos que:
\(V = 20\pi cm³\)
\(h = 5 cm\)
A área lateral é dada por:
\(A_l=2\pi rh\)
Então, para encontrar o r, temos que:
\(V=\pi r^2\cdot h\)
\(20\pi=\pi r^2\cdot5\)
\(\frac{20\pi}{5\pi}=r^2\)
\(r^2=4\)
\(r=\sqrt4\)
\(r\ =\ 2\)
Sabendo que r = 2, então calcularemos a área lateral:
\(A_l=2\pi rh\)
\(A_l=2\pi\cdot2\ \cdot5\)
\(A_l=20\pi\)