A área do cubo é a medida da superfície desse poliedro. A área da base, a área lateral e a área total do cubo estão relacionadas à área do quadrado.
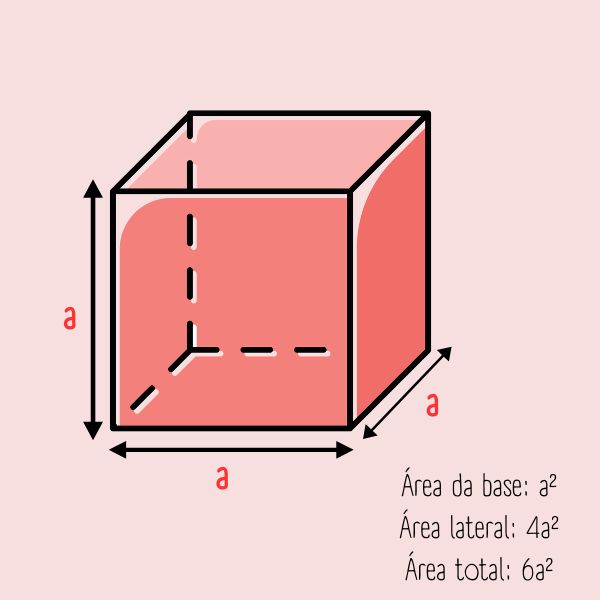
A área do cubo é a medida de sua superfície. Como a superfície do cubo é composta por faces quadradas, é necessário conhecer a área de um quadrado para calcular as áreas do cubo. Nesse contexto, é muito importante não confundir a área total do cubo com seu volume. Enquanto a área total mede a superfície, o volume mede o espaço ocupado por esse sólido.
Leia também: Qual é a fórmula da área do quadrado?
\(Ab=a^2\)
\(Al=4a^2\)
\(At=6a^2\)
Podemos considerar três tipos de áreas do cubo: a área da base, a área lateral e a área total (a soma entre a área da base e a área lateral). Para construir as fórmulas dessas áreas, precisamos compreender a estrutura do cubo.
O cubo, também chamado de hexaedro regular, é um poliedro em que todas as faces são quadrados congruentes. Assim, cada face de um cubo tem a mesma área: a área de um quadrado.
Vamos utilizar como exemplo um cubo em que cada aresta mede a.
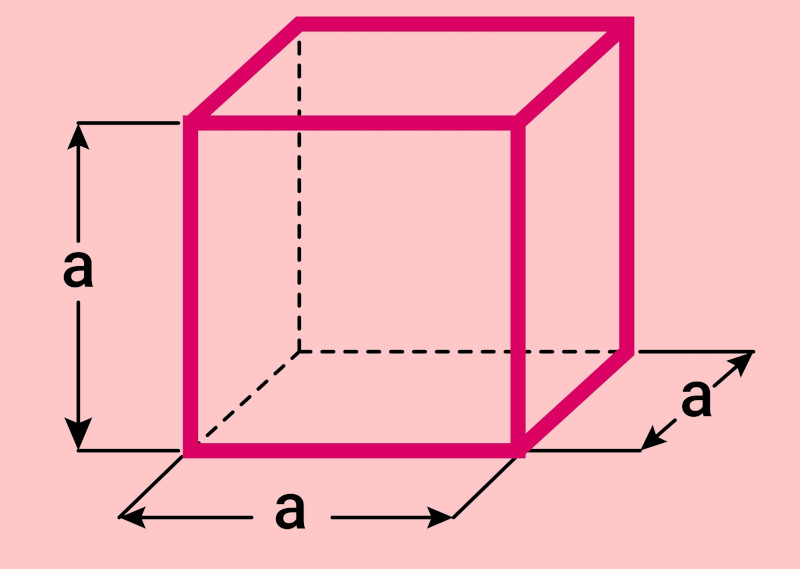
Assim, cada uma das 6 faces do cubo tem a área a²:

Assim, podemos determinar as fórmulas da área da base, área lateral e área total do cubo.
Veja também: Qual é a área de um triângulo?
Para calcular a área da base, a área lateral ou a área do total do cubo, basta identificar a medida da aresta e aplicar a fórmula correspondente. Lembre-se de utilizar a unidade de medida de área apropriada.
Se a medida da aresta do cubo é a, a área da base (Ab) é:
\(Ab=a^2\)
Exemplo: Qual a área da base de um cubo com 3 cm de aresta?
A área da base é a área de 1 face quadrada, assim:
\(Ab=3^2=9\)
Dessa forma, a área da base do cubo é 9 cm².
Se a medida da aresta do cubo é a, a área lateral (Al) é:
\(Al=4a^2\)
Exemplo: Qual a área lateral de um cubo com 3 cm de aresta?
A área lateral é a área de 4 faces quadradas. Assim:
\(Al=4\cdot3^2=4\cdot9=36\)
Logo, a área lateral do cubo é 36 cm².
Se a medida da aresta do cubo é a, a área total (At) é:
\(At=6a^2\)
Exemplo: Qual a área total de um cubo com 3 cm de aresta?
A área total é a área de 6 faces quadradas. Assim:
\(At=6\cdot3^2=6\cdot9=54\)
Portanto, a área total do cubo é 54 cm².
A área de um poliedro é a medida de sua superfície. Já o volume é o espaço que ele ocupa. Imagine que você pegou uma caixa com o formato de um cubo e pintou toda a parte externa (superfície) com uma caneta. A medida da região pintada é a área do cubo.
Agora considere que você quer guardar essa caixa no seu armário. O espaço necessário para guardá-la é o volume dela. Tanto a área total quanto o volume de um cubo estão associados à medida da aresta. Em um cubo de aresta a, a área total é 6a2 e o volume é a3.
Saiba mais: Como calcular o volume do cubo
Questão 1
Qual o comprimento, em cm, da aresta de um cubo com 864 cm² de área total?
a) 10
b) 11
c) 12
d) 13
Resolução
Seja a o comprimento da aresta do cubo, assim:
\(At=864\)
\(6a^2=864\)
\(a^2=\frac{864}{6}\)
\(a^2=144\)
\(a=12\)
Alternativa C
Questão 2
A soma das arestas de um cubo é 84 cm. Qual a área lateral desse cubo em cm²?
a) 49
b) 98
c) 196
d) 294
Resolução
Seja a o comprimento da aresta do cubo, como um cubo tem 12 arestas, segue que:
\(12a=84\)
\(a=\frac{84}{12}=7\)
Logo:
\(Al=4a^2\)
\(Al=4\cdot7^2\)
\(Al=4\cdot49=196\)
Alternativa C
Fontes
MACHADO, P.F. Fundamentos de geometria plana. Belo horizonte: CAED-UFMG, 2012.
REZENDE, E. Q. F.; QUEIROZ, M. L. B. de. Geometria Euclidiana Plana: e construções geométricas. 2ª ed. Campinas: Unicamp, 2008.