O quadrado é um polígono que possui 4 lados com a mesma medida. Para calcular a área do quadrado, basta elevar o comprimento do lado ao quadrado.
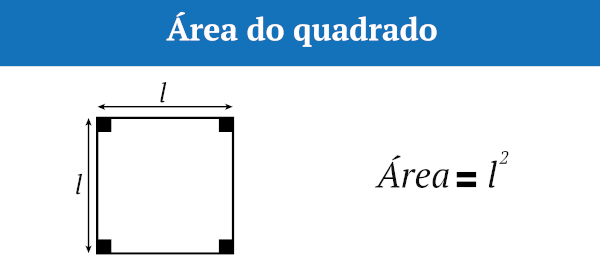
A área do quadrado é igual ao produto da sua base pela sua altura. O quadrado é um quadrilátero que possui todos os lados iguais, por isso, como a sua base e a sua altura possuem a mesma medida, a área do quadrado é igual à medida do lado elevada ao quadrado. Além da área, é possível calcular o comprimento da diagonal do quadrado e a medida do seu perímetro.
Leia também: Como calcular a área de diferentes figuras planas
O quadrado é uma figura plana que possui 4 lados com a mesma medida.
Para calcular a área do quadrado, calculamos a medida do lado ao quadrado.
A fórmula da área do quadrado é:
\(A=l^2\)
Além da área, temos também uma fórmula para calcular o comprimento da diagonal do quadrado:
\(d=\sqrt2\)
O perímetro do quadrado pode ser calculado pela fórmula:
\(P=4l \)
O quadrado é uma figura plana formada por 4 lados congruentes, ou seja, os 4 lados do quadrado possuem a mesma medida.
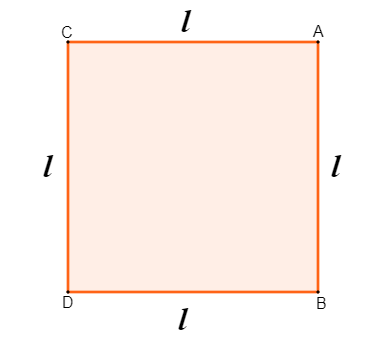
Conhecendo a medida do lado do quadrado, para calcular a área basta calcular o quadrado da medida do lado, ou seja:
\(\mathbf{A=l^2}\)
A → medida da área.
l → comprimento do lado.
Para calcular a medida da área do quadrado, basta substituir o valor do comprimento do seu lado no lugar do l na fórmula.
Exemplo 1:
Um quadrado possui lado medindo 12 cm, então a área desse quadrado é igual a:
Resolução:
Calculando a área, temos que:
\(A=12^2\)
\(A=144\)
Então, a área desse quadrado é de 144 cm².
Exemplo 2:
Calcule a área do quadrado da imagem a seguir:
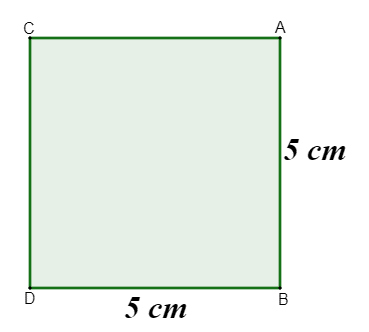
Resolução:
Como a medida do lado é de 5 cm, então para calcular a área elevaremos 5 ao quadrado:
\(A=5^2\)
\(A= 25 \)
A área desse quadrado é 25 cm².
Veja também: Área do triângulo — como calcular?
A diagonal do quadrado é o segmento de reta que liga dois vértices não consecutivos do quadrado. O quadrado possui duas diagonais, que possuem sempre o mesmo comprimento.
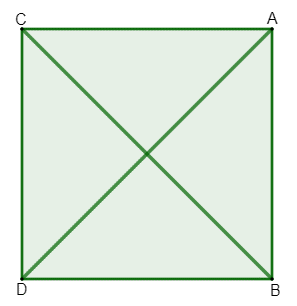
Para calcular a medida da diagonal do quadrado, podemos aplicar o teorema de Pitágoras:
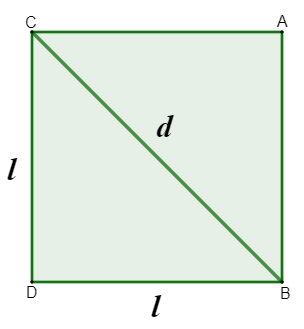
\(d^2=l^2+l^2\)
\(d^2=2l^2\)
\(d=\sqrt{2l^2 }\)
Perceba que, como consequência do teorema de Pitágoras, o comprimento da diagonal do quadrado de lado medindo l pode ser calculado pela fórmula:
\(d=l\sqrt2\)
Exemplo:
Qual é o comprimento da diagonal de um quadrado que possui lados medindo 3 cm?
Resolução:
Se l = 3, então temos que:
\(d=3\sqrt2\)
Logo, o comprimento da diagonal desse quadrado é \(d=3\sqrt2\) cm.
A diferença entre a área e o perímetro, seja do quadrado ou de qualquer outro polígono, é que a área é uma medida que possui duas dimensões, que é o espaço que aquela área ocupa no plano. Já o perímetro é uma medida que possui uma única dimensão, que é o contorno do polígono. Para calcular o perímetro, somamos todos os lados do polígono.
No quadrado de lados medindo l, para calcular o perímetro temos que:
\(\mathbf{P = 4l}\)
Exemplo:
Um quadrado possui lados medindo 3 cm, então qual a medida da sua área e do seu perímetro?
Resolução:
Primeiro, calcularemos a área desse quadrado. Sabemos que:
\(A=l^2\)
\(A=3^2\)
\(A= 9 \)
A área é de 9 cm².
Agora, calcularemos o perímetro desse quadrado:
\(P=4l \)
\(P=4⋅3\)
\(P = 12 \)
O perímetro desse polígono é 12 cm.
Saiba mais: Como saber quantas diagonais tem um polígono?
Questão 1
Uma região possui formato de um quadrado com lado medindo 18 m. Então, podemos afirmar que a área dessa região é de:
A) 72 m²
B) 108 m²
C) 144 m²
D) 288 m²
E) 324 m²
Resolução:
Alternativa E
Calculando a área, temos que:
\(A=l^2\)
\(A=18^2\)
\(A=324\ m^2\)
Questão 2
Seu Antônio decidiu presentear os seus dois filhos com um terreno para cada. Como ele é uma pessoa muito justa, ele consultou ambos, de modo que a área desses terrenos fosse a mesma. Se o terreno de seu primeiro filho é retangular, com lados medindo 48 metros e 12 metros, e sabendo que o terreno do seu segundo filho é um quadrado, então a medida dos lados do terreno do segundo filho é:
A) 20 metros
B) 22 metros
C) 24 metros
D) 30 metros
E) 32 metros
Resolução:
Alternativa C
Calculando a área do terreno retangular, temos que:
\(A = 48 ⋅12 = 576\)
Como o terreno do segundo filho possui mesma área, mas é na forma de um quadrado, então temos que:
\(l^2=576\)
\(l=\sqrt{576}\)
\(l=24 \)
Fonte
DANTE, Luiz Roberto. Matemática: Contexto & Aplicações. 8º ano. São Paulo: Editora Ática, 2021.