O diagrama de Venn é uma forma de representar os conjuntos numéricos geometricamente. Ele auxilia nos estudos dos conjuntos numéricos e nas operações entre eles.
O diagrama de Venn é uma forma que utilizamos para representar os conjuntos numéricos que nos permite visualizar melhor os elementos dos conjuntos e as operações entre eles (união, intersecção e diferença).
Leia também: Sequência numérica — um conjunto formado por números representados em uma ordem
O diagrama de Venn é uma forma de representar os elementos de um ou mais conjuntos. Para fazer essa representação, utilizamos uma forma geométrica fechada e escrevemos os elementos do conjunto dentro dessa forma geométrica. O diagrama de Venn torna mais fácil a visualização das operações entre conjuntos.
Para representar os elementos de um conjunto no diagrama de Venn, colocamos os elementos do conjunto no interior da região fechada.
Veja a seguir uma representação dos elementos do conjunto A: {0, 1, 2, 5, 9, 10} no diagrama de Venn.

Para representar dois conjuntos no diagrama, primeiramente analisamos se eles possuem elementos em comum ou não. Em cada um desses casos, a maneira de representar é diferente.
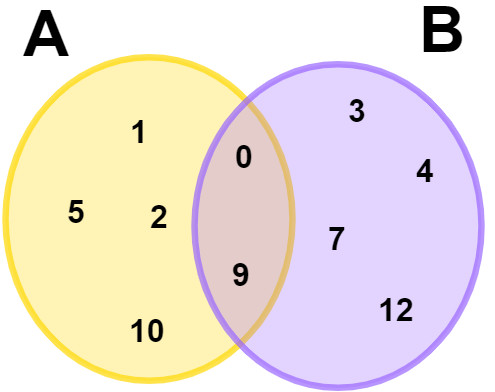
Queremos representar o conjunto A: {0, 1, 2, 5, 9, 10} e o conjunto B: {0, 3, 4, 7, 9, 12}. Note que esses conjuntos possuem elementos em comum. Esses elementos em comum são conhecidos como intersecção e são os elementos que pertencerão aos dois diagramas. Os elementos em comum nesses conjuntos são {0, 9}. Então, representamos esses conjuntos da seguinte maneira:
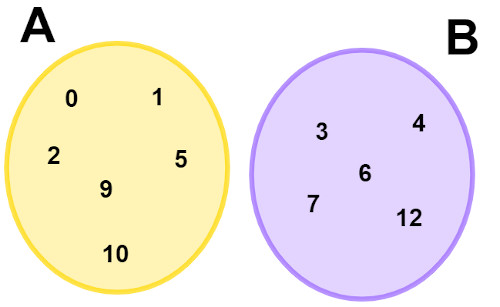
Queremos representar o conjunto A: {0, 1, 2, 5, 9, 10} e o conjunto B: {3, 4, 6, 7, 12}. Quando os conjuntos não possuem elementos em comum, eles são conhecidos como conjuntos disjuntos. A sua representação no diagrama de Venn é feita da seguinte maneira:
As operações entre conjuntos são união, intersecção e diferença. Podemos utilizar o diagrama de Venn para resolver essas operações.
A união entre dois conjuntos é a junção de todos os elementos que pertencem a qualquer um desses conjuntos. Para representar a união entre os conjuntos A e B, utilizamos o símbolo ∪ entre as letras que representam os conjuntos, ou seja, A∪B (lê-se: A união com B).

Exemplo:
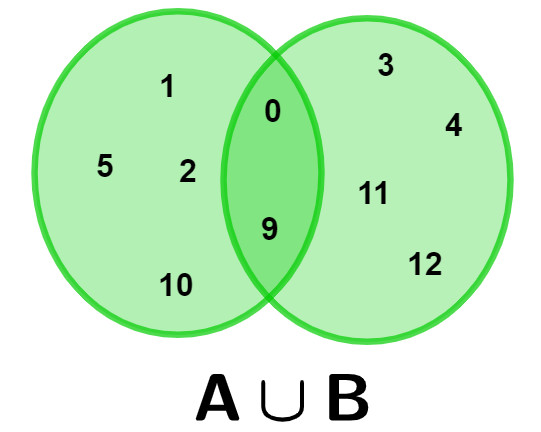
Considere os conjuntos A: {0, 1, 2, 5, 9, 10} e B: {0, 3, 4, 9, 11, 12}. A união desses conjuntos é o conjunto A∪B: {0, 1, 2, 3, 4, 5, 9, 10, 11, 12}.
A intersecção de dois conjuntos é formada pelos elementos que pertencem aos dois conjuntos ao mesmo tempo. O símbolo da intersecção é ∩, então para representar a intersecção entre dois conjuntos escrevemos A∩B (lê-se: A intersecção com B).
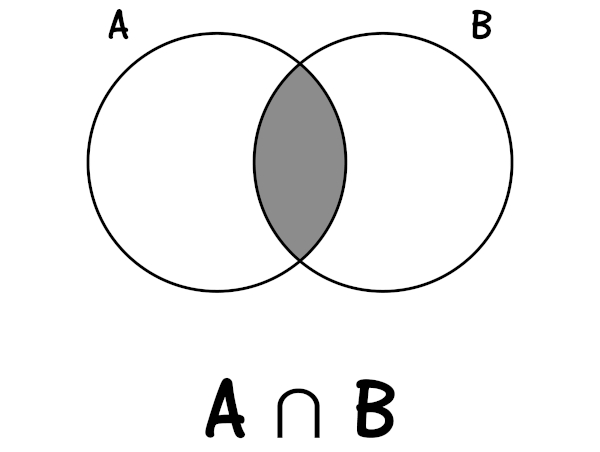
A intersecção dos conjuntos no diagrama de Venn é representada pelos elementos que pertencem tanto à região que delimita o conjunto A quanto à região que delimita o conjunto B.
Exemplo:
Considere os conjuntos A: {0, 1, 2, 5, 9, 10} e B: {0, 3, 4, 9, 11, 12}. A intersecção desses conjuntos é o conjunto A∩B: {0, 9}.

A diferença entre dois conjuntos é representada por A – B. A diferença é composta pelos elementos que pertencem a um dos conjuntos e não pertence ao outro. Por exemplo, na diferença dos conjuntos A – B, encontramos o conjunto formado pelos elementos que pertencem somente ao conjunto A, ou seja, pertencem ao conjunto A mas não pertencem ao conjunto B.
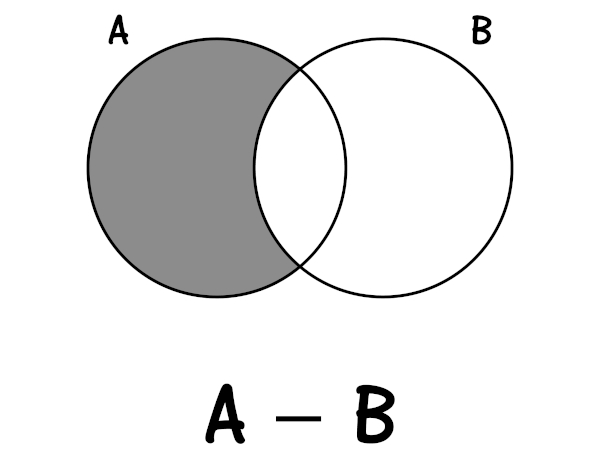
Exemplo:
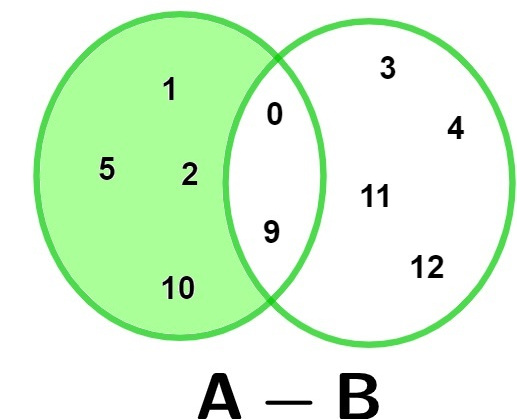
Considere os conjuntos A: {0, 1, 2, 5, 9, 10} e B: {0, 3, 4, 9, 11, 12}. A diferença A – B é o conjunto A – B = {1, 2, 5, 10}, que são os elementos que pertencem ao conjunto A, mas não pertencem ao conjunto B.
Saiba também: Operações com frações — como fazer?
Questão 1
Analise o diagrama de Venn representado na imagem a seguir:

Os elementos pertencentes ao conjunto B – A são:
A) {d, b, c, f, g, h}
B) {a, i, e}
C) {d, b, c}
D) {f, g, h}
E) {a, b, c, d, e, f, g, h, e, i}
Resolução:
Alternativa D
Queremos os elementos que pertencem somente ao conjunto B. São eles: {f, g, h}.
Questão 2
Analise o diagrama a seguir:
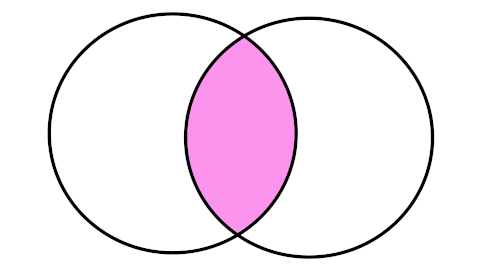
A região destacada é:
A) A união entre os dois conjuntos
B) A diferença entre os dois conjuntos
C) A intersecção entre os dois conjuntos
D) A complementação do primeiro conjunto.
Resolução:
Alternativa C
A região que pertence aos dois conjuntos ao mesmo tempo é conhecida como intersecção.