Clique para aprender uma expressão matemática que pode ser usada no cálculo da soma dos ângulos internos de um polígono.
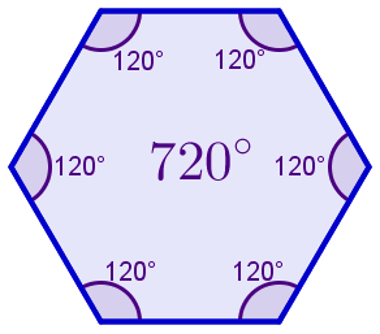
Um polígono é uma figura geométrica formada por segmentos de reta. Essa figura é fechada e nenhum desses segmentos de reta encontra-se a não ser em suas extremidades. Quando o polígono é convexo, é possível descobrir a soma dos seus ângulos internos sem ter que medi-los. Isso é feito por meio de uma fórmula matemática.
Polígono convexo
Um polígono é convexo quando o segmento de reta cujas extremidades são pontos do interior do polígono está inteiramente dentro dele. Em outras palavras, alguns polígonos possuem uma espécie de “boca”, de modo que é possível escolher dois de seus pontos e ligá-los por um segmento de reta que não está inteiramente dentro do polígono. Esses são os chamados não convexos.
Observe a imagem a seguir que mostra um polígono convexo à esquerda e um não convexo à direita.
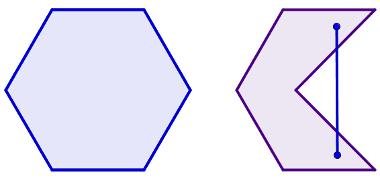
Soma dos ângulos internos
A soma dos ângulos internos de qualquer triângulo é igual a 180°. Tendo isso em mente, podemos pensar em dividir os polígonos convexos em triângulos. Se um polígono pode ser dividido em três triângulos, por exemplo, a soma dos seus ângulos internos é igual a 3 vezes 180.
Para tanto, é preciso criar uma divisão em que a soma dos ângulos dos triângulos seja igual à soma dos ângulos dos polígonos.
É fácil ver que, se escolhermos um vértice de um polígono, as suas diagonais formarão triângulos que cumprem esse pré-requisito. Observe a imagem a seguir:
.jpg)
Essa figura é um hexágono. Repare que, partindo de um mesmo vértice, é possível dividi-lo em quatro triângulos. Para qualquer figura, sempre será possível encontrar n – 3* diagonais partindo do mesmo vértice e, consequentemente, serão formados n – 2* triângulos nesse processo (*n = número de lados do polígono).
Como já foi dito, a soma dos ângulos internos de um polígono é igual ao número de triângulos formados dentro dele multiplicado por 180°. Logo, a soma dos ângulos internos de um polígono convexo é:
S = (n – 2)180°
Exemplos:
Qual a soma dos ângulos internos de um icoságono convexo?
Os icoságonos são polígonos que possuem 20 lados. A soma dos ângulos internos é:
S = (n – 2)180
S = (20 – 2)180
S = 18·180
S = 3280°
Qual é a medida de cada ângulo interno de um icoságono regular?
Polígonos regulares possuem ângulos congruentes. Assim, já sabendo que a soma dos ângulos internos do icoságono é 3280°, cada ângulo dele é igual a:
3280 = 162°
20
Por Luiz Paulo Moreira
Graduado em Matemática
Aproveite para conferir nossas videoaulas sobre o assunto: