Lei dos senos

A lei dos senos é usada para relacionar as medidas de ângulos às medidas de lados de triângulos, não necessariamente daqueles que possuem um ângulo reto. Em outras palavras, elas relacionam ângulos e lados de qualquer triângulo.

As relações trigonométricas básicas – seno, cosseno e tangente – também relacionam medidas de lados a medidas de ângulos de triângulos, entretanto, elas funcionam apenas para triângulos retângulos.

Para usar a lei dos senos, os mesmos valores de seno, cosseno e tangente de ângulos serão usados nos cálculos. Portanto, é de suma importância ter conhecimentos básicos em Trigonometria para conseguir usar esse teorema.

Em vista disso, é bom relembrar também as definições das razões trigonométricas e obter algumas dicas básicas a respeito do seu uso para prosseguir no estudo da lei dos senos.

Razões trigonométricas

As razões trigonométricas são o modo encontrado para relacionar medidas de lados e ângulos. Tendo em mente que a hipotenusa de um triângulo retângulo é o lado que se opõe ao ângulo reto e que os outros dois lados são catetos, podemos fixar um dos outros dois ângulos para ter uma base para os cálculos. Digamos que o ângulo fixado seja α. O cateto que não toca o ângulo α é chamado de cateto oposto a α, e o cateto que o toca é chamado de cateto adjacente ao ângulo α.

Assim, as razões trigonométricas serão:

Sen α = Cateto oposto a α
          hipotenusa

Cos α = Cateto adjacente a α
       hipotenusa

Tg α =   Cateto oposto a α  
         Cateto adjacente a α

É importante salientar que os resultados encontrados nessas razões variam apenas com a variação do ângulo α. Dessa forma, independentemente do comprimento dos catetos ou da hipotenusa, sen30°, por exemplo, sempre será igual a 1/2.

Uma tabela completa com os valores de seno, cosseno e tangente dos ângulos pode ser encontrada clicando aqui.

Lei dos senos

Considere um triângulo qualquer ABC, inscrito em uma circunferência de raio R, conforme a imagem a seguir:

Nessa hipótese, a lei dos senos será a seguinte proporção:

   a    =    b   =   c    = 2R
 senβ     senα    senγ        

Note que a medida de um lado deve ser o numerador de uma fração cujo denominador é o seno do ângulo oposto a esse lado. Essa informação é importante para o uso desse teorema (lei dos senos), uma vez que nos ajuda a localizar lados e ângulos nos cálculos.

Exemplo

Calcule o valor de x do triângulo a seguir:

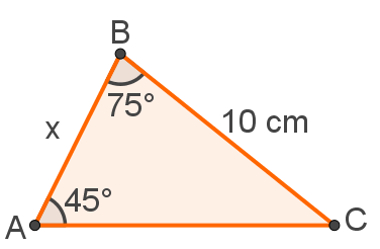
Solução:

Observe que x está oposto ao ângulo que não possui medida. Sabendo que a soma dos ângulos internos de um triângulo é igual a 180° e que esse triângulo já possui 45 + 75 = 120°, então, o ângulo oposto a x mede 60°. Perceba também que o ângulo oposto a 10 mede 45°. Portanto:

      x    =      10    
sen60°    sen45°

Usando a propriedade fundamental das proporções, teremos:

x·sen45° = 10·sen60°

x·√2 = 10·√3
    2           2

x√2 = 10√3

x = 10√3
     √2

Racionalizando o segundo membro, teremos:

x = 10√3√2
     2

x = 10√6
     2

Aproveite para conferir nossas videoaulas sobre o assunto: