Volume do prisma

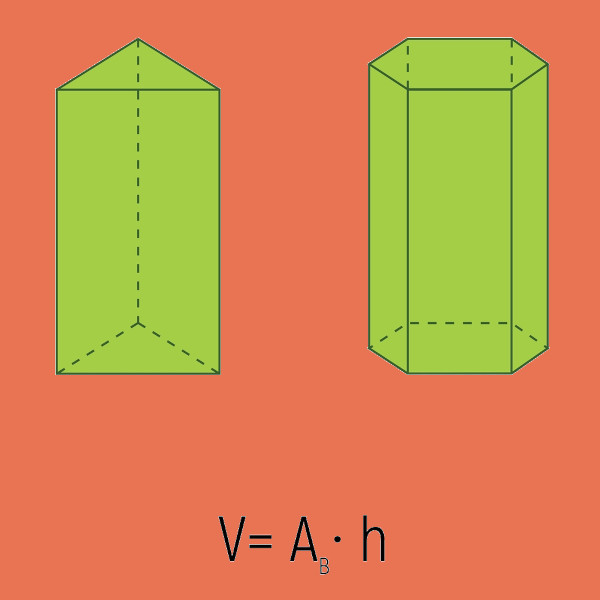
Volume do prisma é o espaço ocupado por esse sólido geométrico. Prisma é um poliedro com duas bases congruentes e faces laterais retangulares. O volume de um prisma é o resultado da multiplicação entre a área da base e a altura.

Leia também: Fórmulas de volumes de sólidos geométricos

Resumo sobre volume do prisma

• O espaço ocupado por um prisma é o seu volume.
• Um prisma é formado por duas bases congruentes e por faces laterais retangulares.
• A área de uma das bases do prisma é representada por A_b e a altura, por h.
• A fórmula do volume de um prisma é:

\(V=A_b\cdot h\)

• O formato da base (triângulo, quadrado, retângulo, pentágono etc.) determina o tipo de prisma.

Videoaula sobre o volume do prisma

Fórmula do volume do prisma

Considere um prisma com área da base A_b e altura (distância entre as bases) h. Assim, a fórmula do volume do prisma é:

\(V_{\mathrm{prisma}}=A_b\cdot h\)

Portanto, o volume de um prisma é o resultado da multiplicação entre a área de uma das bases e a altura.

Como calcular o volume do prisma?

Para calcular o volume de um prisma, precisamos descobrir duas informações: a área da base e a altura. O cálculo da área da base dependerá de qual polígono compõe a base do prisma, e a altura do prisma é a distância entre as bases.

Vejamos alguns exemplos de como calcular o volume do prisma para diferentes tipos de prismas.

• Volume do prisma triangular

Um prisma em que as bases são triângulos, como na imagem abaixo, é chamado de triangular.

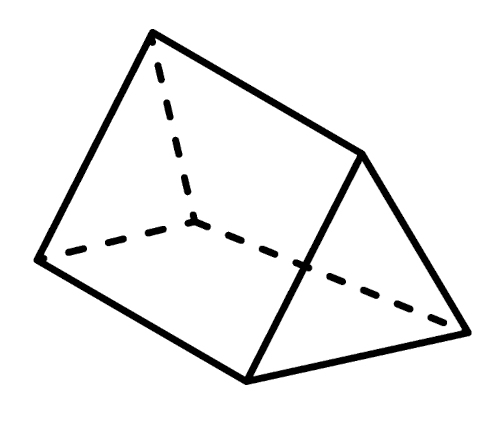
Exemplo: Considere um prisma em que as bases são triângulos equiláteros. Se a aresta da base mede 2 cm e a altura 5 cm, qual o volume desse prisma?

Nesse caso, a área da base é a área de um triângulo equilátero de lado 2 cm. Assim:

\(A_b=\frac{l^2\sqrt3}{4}\)

\(A_b=\frac{2^2\sqrt3}{4}\)

\(A_b=\sqrt3\)

Como a altura h do prisma é 5 cm, segue que o volume desse sólido é:

\(V=A_b\cdot h\)

\(V=5\sqrt3 cm³\)

• Volume do prisma de base quadrada

Como o nome sugere, as bases nesse tipo de prisma são quadrados.

Exemplo: Qual o volume de um prisma de 7 cm de altura em que as bases são quadrados com 3 cm de lado?

A área da base desse prisma é a área de um quadrado de lado 3 cm. Assim:

\(A_b=l^2\)

\(A_b=3^2=9 cm²\)

Logo, como h=7 cm, temos que:

\(V=A_b\cdot h\)

\(V=9\cdot7=63 cm³\)

• Volume do prisma reto de base retangular (paralelepípedo ou bloco retangular)

Um paralelepípedo reto é um prisma com bases retangulares, como indicado na imagem.

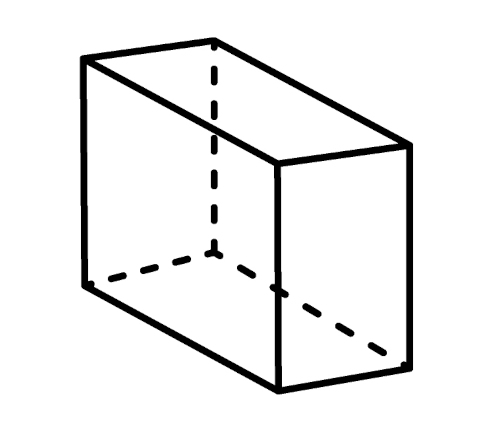
Exemplo: Qual o volume de prisma com 6 cm de altura em que as bases são retângulos de dimensão 5 cm x 3 cm?

A área da base desse prisma é a área de um retângulo com 5 cm de comprimento e 3 cm de largura. Portanto:

\(A_b=\mathrm{comprimento\ x\ largura}\)

\(A_b=5\cdot3=15 cm²\)

Assim, como a altura h  do prisma é 6 cm, temos que:

\(V=A_b\cdot h\)

\(V=15\cdot6=90 cm³\)

• Volume do prisma pentagonal

Um prisma em que a base é um pentágono (polígono com 5 lados) é chamado de prisma pentagonal.

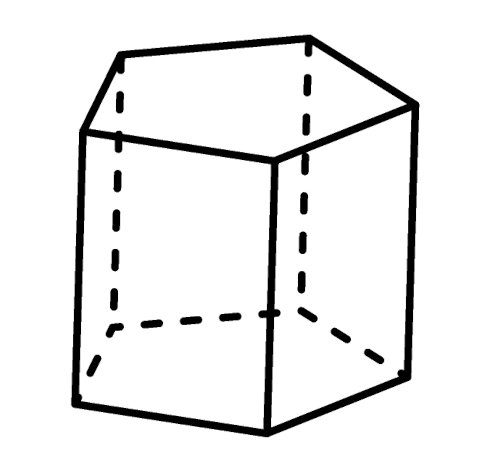
Exemplo: Considere um prisma com 10 cm de altura em que as bases são pentágonos regulares com 5 cm de lado e 3,44 cm de apótema. Qual o volume desse prisma?

Nesse exemplo, a área da base é a área de um pentágono regular com 5 cm de lado e 3,44 cm de apótema. Assim:

\(A_b=5\cdot\left(\frac{l\cdot a}{2}\right)\)

\(A_b=5\cdot\left(\frac{5\cdot3,44}{2}\right)\)

\(A_b=43 cm²\)

Portanto, como a altura h  é igual a 10 cm, temos que:

\(V=A_b\cdot h\)

\(V=43\cdot10=430 cm³\)

Princípio de Cavalieri

Sejam S₁ e S₂ dois sólidos geométricos de mesma altura h com bases congruentes sobre um plano β. Considere um plano α  arbitrário, paralelo a β , que é secante aos dois sólidos, conforme a imagem.

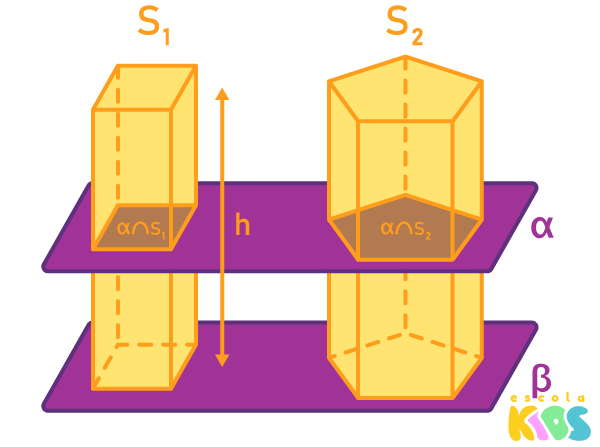
A região α∩S₁ é a interseção do sólido S₁ com o plano α  e a região α∩S₂ é a interseção do sólido S₂ com o plano α .

Se a área de α∩S₁ é igual à área de α∩S₂, então o volume do sólido S₁ é igual ao volume do sólido S₂. Esse é o princípio de Cavalieri, um resultado matemático utilizado para a construção de fórmulas para volumes de sólidos geométricos.

Leia também: Como calcular o volume da pirâmide

Exercícios sobre volume do prisma

Questão 1

(Enem) Uma fábrica produz barras de chocolates no formato de paralelepípedos e de cubos, com o mesmo volume. As arestas da barra de chocolate no formato de paralelepípedo medem 3 cm de largura, 18 cm de comprimento e 4 cm de espessura.

Analisando as características das figuras geométricas descritas, a medida das arestas dos chocolates que têm o formato de cubo é igual a

a) 5 cm.

b) 6 cm.

c) 12 cm.

d) 24 cm.

e) 25 cm.

Resolução

O volume das barras de chocolates no formato de paralelepípedos é igual ao produto entre a área da base retangular (que é o produto da largura e do comprimento) e a espessura:

\(V_{paralelepípedo}=3⋅18⋅4=216\)

Seja a  a medida da aresta das barras de chocolate em formato de cubo. Como essas barras têm o mesmo volume que as barras em formato de paralelepípedo e o volume de um cubo é a3 , segue que:

\(V_{\mathrm{cubo}}=216\)

\(a^3=216\)

\(a=\sqrt[3]{216}=6\)

Alternativa B

Questão 2

Uma caixa tem o formato de um paralelepípedo reto com dimensões 18 cm x 14 cm x 10 cm. Qual o volume dessa caixa em centímetros cúbicos?

a) 252

b) 262

c) 420

d) 1252

e) 2520

Resolução

A base dessa caixa é um retângulo com 18 centímetros de comprimento e 14 centímetros de largura. Assim:

\(A_b=18\cdot14=252 cm²\)

Como a altura da caixa mede 10 cm, segue que:

\(V=252\cdot10=2520 cm³\)

Alternativa E

Fontes:

DOLCE, O; POMPEO, J. N. Fundamentos de matemática elementar, Vol 10: Geometria espacial - Posição e métrica. 7ª ed. Santos: Atual, 2013.

TOSE, M. de T. Volume: Princípio de Cavalieri no Ensino Médio. Dissertação (Mestrado) – Programa de Pós-Graduação em Matemática em Rede Nacional (PROFMAT), Universidade Estadual Paulista, 2017. Disponível em  http://hdl.handle.net/11449/149744 .