Polígonos regulares

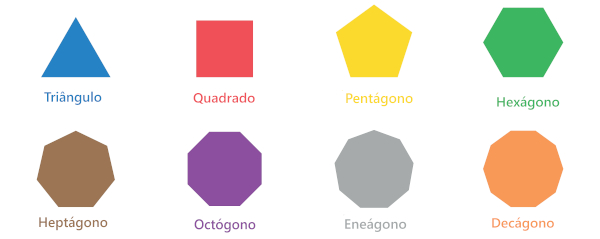
Polígonos regulares são os polígonos convexos em que todos os lados e todos os ângulos são congruentes, ou seja, têm a mesma medida. O polígono regular de 3 lados é o triângulo equilátero e o de 4 lados é o quadrado. Os demais polígonos regulares têm apenas o acréscimo do termo “regular” na nomenclatura: pentágono regular, hexágono regular etc.

Leia também: O que são polígonos semelhantes?

Resumo sobre polígonos regulares

• Polígono regular é um polígono convexo com todos os lados e ângulos congruentes.

• Todo polígono regular é inscritível e circunscritível.

• O perímetro P de um polígono regular com n lados de medida l é dado por:

\(P=n ⋅l\)

• A área A de um polígono regular com n lados de medida l e apótema h é dada por:

\(A=n⋅\frac{l⋅h}2\)

• O ângulo interno \(a_i\) de um polígono regular com n lados é dado por:

\(a_i=\frac{(n-2)⋅180°}n\)

• O ângulo externo ae de um polígono regular com n lados é dado por:

\(a_e=\frac{360°}n\)

Videoaula sobre polígonos regulares

O que são polígonos regulares?

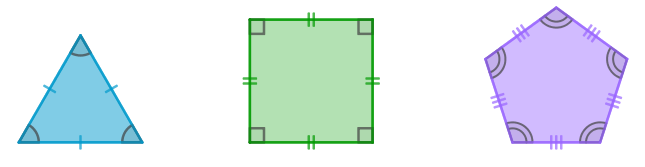
Um polígono convexo que possui todos os lados e ângulos congruentes é chamado de polígono regular. Na imagem abaixo, temos, respectivamente, o triângulo regular (conhecido como triângulo equilátero), o quadrilátero regular (quadrado) e o pentágono regular.

Quais são as propriedades dos polígonos regulares?

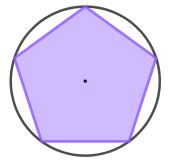
• Propriedade 1: Todo polígono regular é inscritível.

Isso significa que, dado um polígono regular, existe uma circunferência que contém todos os vértices do polígono. O raio dessa circunferência é a distância do centro do polígono a um dos vértices.

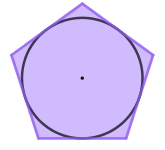
• Propriedade 2: Todo polígono regular é circunscritível.

Isso significa que, dado um polígono regular, existe uma circunferência que tangencia todos os lados do polígono. O raio dessa circunferência é a distância do centro do polígono a um dos lados.

Veja também: Polígonos inscritos e circunscritos — elementos e propriedades

Qual o perímetro dos polígonos regulares?

O perímetro de um polígono é a soma das medidas de seus lados. No caso de um polígono regular, como todos os lados são congruentes, podemos construir uma expressão para o cálculo do perímetro.

Em um polígono com n lados de medida l, o perímetro P é dado por:

\(P=n⋅l\)

Exemplo:

Qual o perímetro de um triângulo equilátero de lado 2 cm?

\(P=2\ cm+2\ cm+2\ cm=6\ cm\)

Note que \(P=3⋅2\ cm=6\ cm\).

Apótema de um polígono regular

O apótema de um polígono é o segmento perpendicular a um dos lados com extremidade no centro. No caso dos polígonos regulares, o apótema é o raio da circunferência inscrita.

Qual a área dos polígonos regulares?

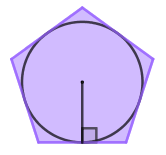
Todo polígono regular pode ser dividido em triângulos isósceles congruentes por segmentos que unem o centro do polígono aos vértices. Consequentemente, a área de um polígono regular é igual à soma das áreas dos triângulos.

Vejamos um exemplo com o pentágono regular. Seja l o lado do pentágono e h o apótema.

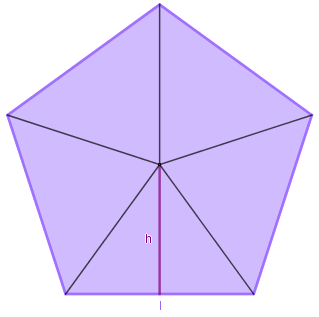
Note que o pentágono regular pode ser dividido em 5 triângulos congruentes de base l e altura h. Portanto, a área desse pentágono é:

\(A=5⋅\frac{l⋅h}2\)

Perceba que podemos generalizar essa ideia. Considere um polígono regular com n lados, em que cada um mede l. Assim, podemos dividir esse polígono em n triângulos congruentes de base l e altura h. Dessa forma, a área é:

\(A_{polígono\ regular} =n⋅\frac{l⋅h}2\)

Observação: Como n⋅l é o perímetro P do polígono, também podemos escrever:

\(A_{polígono\ regular} =n⋅\frac{l⋅h}2=\frac{n⋅l⋅h}2\)

\(A_{polígono\ regular} =\frac{P⋅h}2\)

Exemplo:

Qual a área aproximada de um octógono regular cujos lados medem 0,5 cm e o apótema mede aproximadamente 0,6 cm?

Como n = 8, l = 0,5 cm e h ≈ 0,6 cm, temos que:

\(A=n⋅\frac{l⋅h}2\)

\(A≈8⋅\frac{0,5⋅0,6}2\)

\(A≈1,2\ cm^2\)

Ângulos internos dos polígonos regulares

Todos os ângulos internos de um polígono regular são congruentes, ou seja, têm a mesma medida. Portanto, se \(a_i\) é a medida do ângulo interno de um polígono de n lados, então a soma S dos ângulos internos é \(S=n⋅a_i\) e, assim:

\(a_i=\frac{S}n\)

Contudo, todo polígono regular é convexo e há uma fórmula para a soma S dos ângulos internos de um polígono convexo. Vejamos como melhorar essa expressão.

→ Soma dos ângulos internos de um polígono regular

A soma S dos ângulos internos de um polígono convexo de n lados é dada por:

\(\mathbf{S=(n-2)⋅180°}\)

Portanto, substituindo essa fórmula na expressão do tópico anterior, temos que a medida do ângulo interno de um polígono regular é dada por:

\(a_i=\frac{(n-2)⋅180°}n\)

Exemplo:

Determine a medida de cada ângulo interno de um hexágono regular e a soma dos ângulos internos.

Como n = 6, temos que:

\(S=(6-2)⋅180°= 720°\)

\(a_i=\frac{720°}6=120°\)

Ângulos externos dos polígonos regulares

Todos os ângulos externos de um polígono regular são congruentes. Como os polígonos regulares são convexos e a soma dos ângulos externos de um polígono convexo é 360°, então a medida de cada ângulo externo \(a_e\) de um polígono regular é dada por:

\(a_e=\frac{360°}n\)

Saiba mais: Como encontrar a diagonal dos polígonos

Diferença entre polígono regular e polígono irregular

Um polígono é chamado de irregular (ou não regular) se não possui todos os lados congruentes ou todos os ângulos congruentes. Exemplos de polígonos irregulares são o retângulo (pois os lados não são congruentes) e o losango (pois os ângulos não são congruentes).

Exercícios resolvidos sobre polígonos regulares

Questão 1

Qual a medida de cada ângulo interno de um eneágono regular?

a) 60°

b) 90°

c) 108°

d) 120°

e) 140°

Resolução: letra E

Eneágono regular é o polígono regular com 9 lados. Assim:

\(a_i=\frac{(9-2)⋅180°}9=140°\)

Questão 2

Se o perímetro de um heptágono regular é igual a 35 cm, o lado desse polígono mede

a) 5 cm.

b) 7 cm.

c) 10 cm.

d) 11 cm.

e) 13 cm.

Resolução: letra A

Heptágono regular é o polígono regular com 7 lados, portanto:

\(P=n⋅l\)

\(35=7⋅l\)

\(l=5\ cm\)