Clique e descubra o que é uma função do segundo grau, aprenda a calcular suas raízes e seu vértice e a construir seu gráfico.
Uma função do segundo grau, também conhecida como função quadrática, é definida pela regra a seguir:
y = f(x) = ax2 + bx + c
Em que a, b e c são números reais e a ≠ 0.
Assim como as funções do primeiro grau, as funções quadráticas também podem ter seu gráfico construído. Entretanto, essa é uma tarefa mais difícil e depende de alguns conhecimentos prévios, que serão discutidos a seguir.
Parábola e sua concavidade
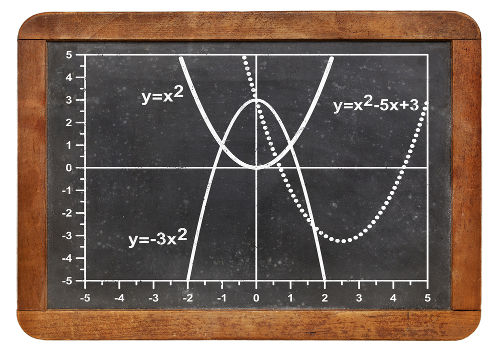
O gráfico da função do segundo grau é uma parábola. A concavidade de uma parábola, que representa uma função do segundo grau, é definida pelo valor numérico do coeficiente a na regra da função. Se a > 0, a concavidade da parábola é voltada para cima. Se a
Na função f(x) = 2x2, perceba que a = 2, o qual é um número maior que zero. Portanto, a concavidade da parábola é voltada para cima:
Já na função g(x) = – 2x2, perceba que a = – 2, o qual é um número menor que zero. Portanto, a concavidade da parábola é voltada para baixo.
Vértice de uma parábola
Quando uma parábola tem concavidade voltada para cima, um de seus pontos fica mais abaixo de todos os outros. Esse ponto é chamado de vértice. Quando a parábola tem concavidade voltada para baixo, um de seus pontos fica mais acima de todos os outros. Esse ponto é chamado de vértice.
Supondo que o vértice V de uma parábola possui as coordenadas: V = (xv, yv), para encontrar o valor numérico delas, podemos usar as seguintes fórmulas:
xv = – b
2a
yv = – Δ
4a
Em que a, b e Δ são obtidos a partir dos coeficientes da função. Por exemplo, na função f(x) = x2 – 6x + 8, teremos as coordenadas de V = (3, – 1), pois:
xv = – (– 6)
2
xv = 6
2
xv = 3
Para yv, devemos calcular primeiramente:
Δ = b2 – 4·a·c
Δ = (– 6)2 – 4·1·(8)
Δ = 36 – 32
Δ = 4
Agora, usaremos a fórmula para yv:
yv = – Δ
4a
yv = – 4
4
yv = – 1
Raízes de uma função do segundo grau
As raízes de uma função são os valores do domínio relacionados a zero no contradomínio. Em outras palavras, fazemos y ou f(x) = 0 para descobrir os valores de x que tornam essa sentença verdadeira. As raízes de uma função também são os pontos de encontro do gráfico dessa função com o eixo x.
Assim, as coordenadas das raízes definem os pontos A = (x’, 0) e B = (x’’, 0).
Para encontrar as raízes da função do segundo grau, pode-se usar a fórmula de Bháskara ou qualquer outro método capaz de calcular raízes de uma função.
Exemplo: As raízes da função f(x) = x2 – 6x + 8 são:
f(x) = x2 – 6x + 8
0 = x2 – 6x + 8
Δ = b2 – 4·a·c
Δ = (– 6)2 – 4·1·(8)
Δ= 36 – 32
Δ= 4
x = – b ± √Δ
2a
x = – (– 6) ± √4
2
x = 6 ± 2
2
x’ = 6 + 2 = 8 = 4
2 2
x’’ = 6 – 2 = 4 = 2
2 2
S = {2, 4}
E essas raízes são os dois pontos da função: A = (2,0) e B = (4,0)
Ponto de encontro da função com o eixo y
O gráfico de uma função é construído no plano cartesiano. As funções do segundo grau sempre se encontram com o eixo y desse plano no ponto (0,c). Isso significa que a coordenada c da função é o ponto de encontro dela com o eixo y.
Gráfico da função do segundo grau
Para construir o gráfico de uma função do segundo grau, será necessário seguir o passo a passo:
1º – Descobrir sua concavidade;
2º – Encontrar as coordenadas do vértice;
3º – Encontrar as coordenadas das raízes da função;
4º – Encontrar dois pontos “aleatórios” pertencentes à função (se necessário).
Exemplo: Vamos construir o gráfico da função f(x) = x2 – 6x + 8 usando esse passo a passo.
1º – A concavidade da parábola é voltada para cima, pois a = 1 > 0.
2º – As coordenadas do vértice são: V = (3, – 1) e os procedimentos para encontrá-las estão descritos acima.
3º – Encontrar as raízes da função. Observe que algumas funções do segundo grau não terão duas raízes reais distintas. Isso acontece quando Δ = 0 ou Δ gráfico.
Assim, nesse exemplo, já podemos marcar os pontos A, B e V, que são as raízes e o vértice. O gráfico dessa função será:
4º – Quando a função não possui duas raízes reais distintas, observe a coordenada x de seu vértice, escolha x = xv + 1 e x = xv – 1, coloque esses valores no lugar de x na função e descubra a coordenada y referente a eles. Marque os dois pontos obtidos no plano cartesiano, juntamente com o vértice e desenhe o gráfico.
Exemplo: Na função f(x) = 2x2, Δ = 0; xv = 0 e yv = 0. Assim, escolheremos x = 1 e x = – 1 para calcular outros dois pontos que não são as raízes e marcá-los no gráfico.
f(x) = 2x2
f(1) = 2·12
f(1) = 2·1
f(1) = 2
f(– 1) = 2·(–1)2
f(– 1) = 2·1
f(– 1) = 2
Então, os pontos A e B dessa função serão: A = (1, 2) e B = (– 1 , 2), e seu gráfico será: