Clique para aprender o que é função, domínio, imagem e as representações possíveis para funções!
Uma função é uma regra que relaciona dois conjuntos de forma que cada elemento do primeiro conjunto possua um único representante no segundo conjunto. Essa regra também é conhecida como lei de formação, e os elementos desses conjuntos são chamados de variáveis.
Domínio e Imagem de uma função
O primeiro conjunto dessa definição contém números que, de certa maneira, dominam os seus possíveis resultados da função. Por esse motivo, esse conjunto é chamado de domínio e seus elementos são chamados de variáveis independentes e, geralmente, são representados pela letra x.
Já o segundo conjunto contém elementos que variam de acordo com a variação dos elementos do domínio. Portanto, o segundo conjunto é composto por “imagens” das variáveis independentes, uma vez que todo esse conjunto é apenas resultado de cada elemento do primeiro conjunto avaliado na lei de formação da função. Esse fato nomeia o segundo conjunto como imagem e seus elementos como variáveis independentes. Estas, geralmente, são representadas pela letra y.
Para definir uma função, é necessário que esses dois conjuntos estejam bem definidos. Para tanto, basta definir a lei de formação e o domínio.
As variáveis são, assim como nas expressões algébricas, números representados por letras. A diferença está no fato de que a variável pode assumir qualquer valor dentro do conjunto a que ela pertence, ou seja, nas expressões algébricas, a incógnita é um número desconhecido; nas funções, a variável é um número qualquer pertencente a um conjunto numérico.
Representações da função
→ Representação algébrica
A representação algébrica de uma função é uma fórmula matemática que relaciona cada elemento de um conjunto a outro. Essa representação é dada pelo símbolo “f(x)” ou pela letra “y” com uma expressão algébrica na sequência. Seguem abaixo alguns exemplos de leis de formação de funções em sua forma algébrica.
f(x) = 2x
y = 2x
Observe que as duas leis de formação acima se referem à mesma função. Se definirmos o domínio dessa função como o conjunto dos números naturais, a sua imagem será o conjunto dos números pares. Observe:
f(x) = 2·x
f(1) = 2·1 = 2
f(2) = 2·2 = 4
f(3) = 2·3 = 6
…
Substituindo x pelos números naturais 1, 2, 3, …, sempre obteremos números pares por meio da lei de formação f(x) = 2x. Logo, 1, 2, 3 … são os elementos que compõem o domínio, e 2, 4, 6 … são os elementos que compõem a imagem.
→ Representação por diagrama
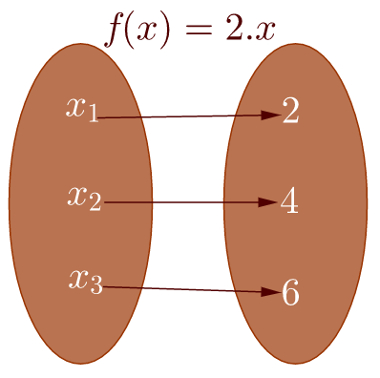
Quando a função possui poucos elementos, é possível desenhar diagramas e ligar todos os seus elementos. No exemplo abaixo, utilizaremos a mesma função do exemplo anterior, mas com domínio restrito a três elementos. Observe:

Representação de uma função cujo domínio é D = {1, 2, 3} e a imagem é I = {2, 4, 6}
Grau de uma função
O grau de uma função é atribuído de acordo com o número de variáveis que estão sendo multiplicadas. Caso a função seja dada apenas em uma variável (caso mais frequente), seu grau pode ser avaliado pelo maior expoente encontrado entre suas variáveis. Por exemplo: a função f(x) = 2x tem grau 1, pois 1 é o maior expoente de uma variável presente nessa função. Já a função f(x) = x4 – 4x2 possui grau 4.
Por Luiz Paulo Moreira
Graduado em Matemática