A classificação do triângulo pode ser feita por meio das características de seus lados ou de seus ângulos internos.

A classificação de um triângulo é uma maneira de categorizá-lo. Todos os triângulos possuem três lados e três ângulos, mas dependendo das características desses lados e ângulos, podemos identificar diferentes tipos de triângulo.
Existem duas formas de classificar um triângulo: a primeira considera aspectos sobre os lados do triângulo, e a segunda considera aspectos sobre os ângulos. No primeiro caso, um triângulo pode ser equilátero, isósceles ou escaleno; no segundo caso, pode ser acutângulo, retângulo ou obtusângulo.
Leia também: Quais são os casos de semelhança de triângulos?
Todo triângulo possui três vértices, três lados e três ângulos.
Em todo triângulo, o lado maior é oposto ao ângulo maior e o lado menor é oposto ao ângulo menor.
A soma dos ângulos internos de qualquer triângulo é 180°.
Um triângulo é chamado de equilátero se todos os lados possuem a mesma medida.
Um triângulo é chamado de isósceles se dois lados possuem a mesma medida.
Um triângulo é chamado de escaleno se todos os lados possuem medidas diferentes.
Um triângulo é chamado de acutângulo se todos os ângulos são agudos.
Um triângulo é chamado de retângulo se possui um ângulo reto.
Um triângulo é chamado de obtusângulo se possui um ângulo obtuso.
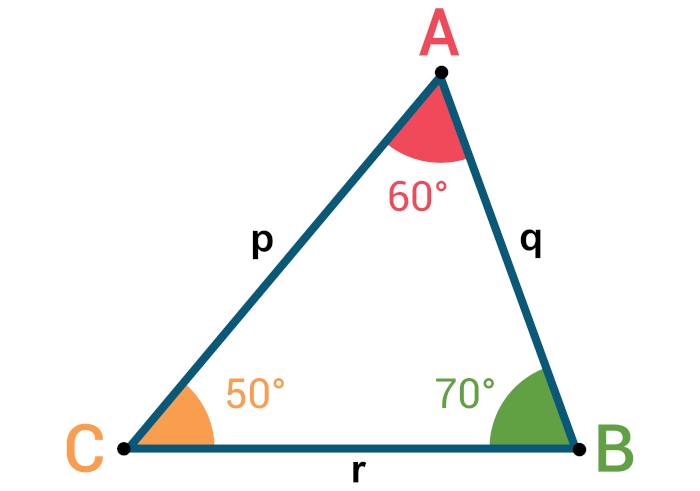
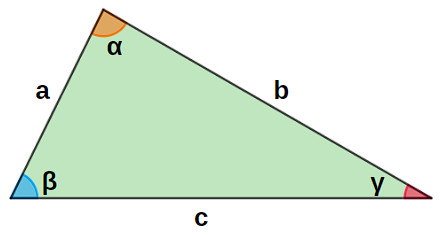
Todo triângulo possui três lados, três vértices e três ângulos internos. Os lados são indicados por segmentos de reta, os vértices são os pontos em que os lados se encontram e os ângulos internos são as aberturas formadas no encontro de dois lados.
Existem propriedades que são válidas para todos os triângulos. Vamos conhecer algumas.
A medida de um lado é sempre menor que a soma das medidas dos outros dois lados. Essa propriedade é chamada de condição de existência de um triângulo.
O lado maior é oposto ao ângulo maior, e o lado menor é oposto ao ângulo menor.
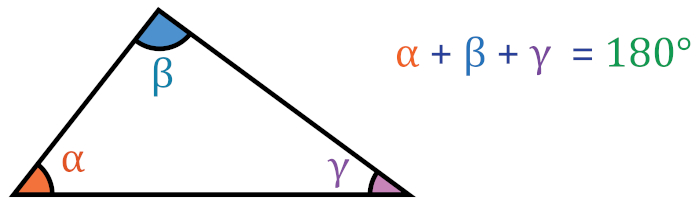
A soma dos ângulos internos mede 180°.
Os triângulos são classificados em relação aos lados e em relação aos ângulos.
Em relação aos lados, um triângulo pode ser equilátero, isósceles ou escaleno.
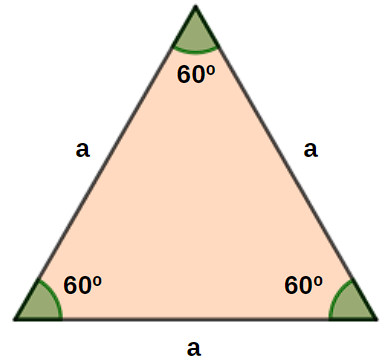
Um triângulo é um triângulo equilátero se todos os lados possuem a mesma medida. Como consequência, nesse tipo de triângulo, os três ângulos medem 60°.
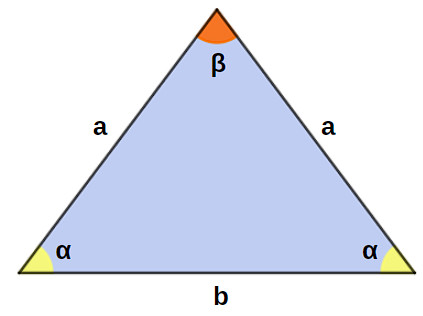
Um triângulo é um triângulo isósceles se dois lados possuem a mesma medida. Como consequência, nesse tipo de triângulo, os lados iguais levam a ângulos com a mesma medida.
Um triângulo é um triângulo escaleno se os três lados possuem medidas diferentes. Como consequência, nesse tipo de triângulo, os três ângulos também possuem medidas diferentes.
|
Exemplo de fixação |
|
Classifique os triângulos abaixo em equilátero, isósceles ou escaleno.
|
|
Resolução: O triângulo a é escaleno, pois todos os lados têm medidas diferentes. O triângulo b é isósceles, pois dois lados têm a mesma medida. O triângulo c é equilátero, pois todos os lados têm a mesma medida. |
Em relação aos ângulos, um triângulo pode ser acutângulo, retângulo ou obtusângulo.
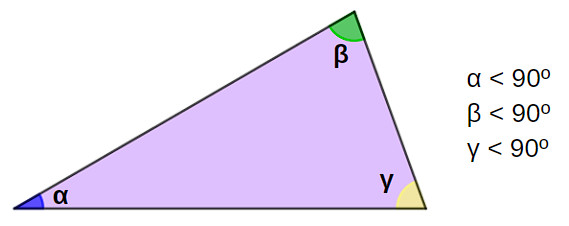
Um triângulo é um triângulo acutângulo se todos os ângulos são agudos, ou seja, têm medida menor que 90°.
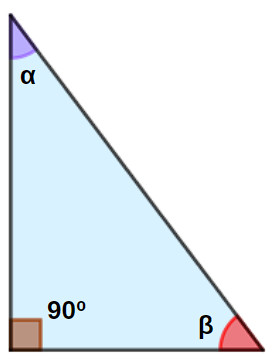
Um triângulo é um triângulo retângulo se possui um ângulo reto, ou seja, com medida igual a 90°.
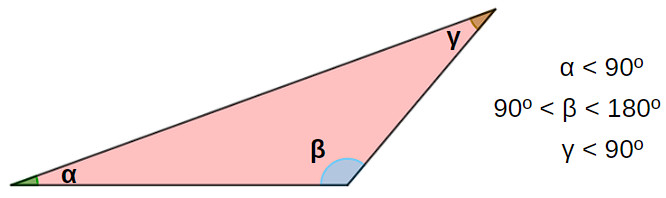
Um triângulo é um triângulo obtusângulo se possui um ângulo obtuso, ou seja, com medida entre 90° e 180°.
|
Exemplo de fixação |
|
Classifique os triângulos abaixo em acutângulo, retângulo ou obtusângulo.
|
|
Resolução: O triângulo a é retângulo, pois possui um ângulo de 90°. O triângulo b é obtusângulo, pois possui um ângulo obtuso. O triângulo c é acutângulo, pois todos os ângulos são agudos. |
Veja também: Como calcular a área de um triângulo?
Questão 1
(Enem) O remo de assento deslizante é um esporte que faz uso de um barco e dois remos do mesmo tamanho. A figura mostra uma das posições de uma técnica chamada afastamento.
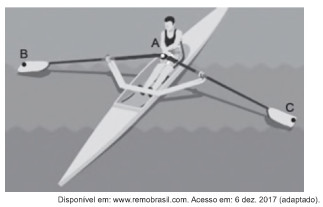
Nessa posição, os dois remos se encontram no ponto A e suas outras extremidades estão indicadas pelos pontos B e C. Esses três pontos formam um triângulo ABC, cujo ângulo \(BÂC\) tem medida de 170°.
O tipo de triângulo com vértices nos pontos A, B e C, no momento em que o remador está nessa posição, é
A) retângulo escaleno.
B) acutângulo escaleno.
C) acutângulo isósceles.
D) obtusângulo escaleno.
E) obtusângulo isósceles.
Resolução:
Alternativa E
Como os dois remos, indicados por AB e AC, são do mesmo tamanho, então ABC é um triângulo isósceles. Ainda, como \(BÂC=170°\), o triângulo ABC é obtusângulo.
Questão 2
(Enem) Um professor, ao fazer uma atividade de origami (dobraduras) com seus alunos, pede para que estes dobrem um pedaço de papel em forma triangular, como na figura a seguir, de modo que M e N sejam pontos médios respectivamente de AB e AC, e D, ponto do lado BC, indica a nova posição do vértice A do triângulo ABC.
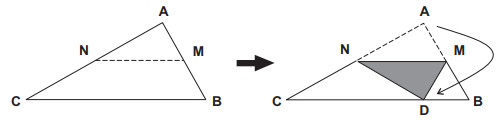
Se ABC é um triângulo qualquer, após a construção, são exemplos de triângulos isósceles os triângulos
A) CMA e CMB.
B) CAD e ADB.
C) NAM e NDM.
D) CND e DMB.
E) CND e NDM.
Resolução:
Alternativa D
Se N é ponto médio de AC, então CN = NA. Se M é ponto médio de AB, então AM = MB.
Após a dobradura, observe que o segmento ND possui a mesma medida do antigo segmento NA. Além disso, o segmento MD possui a mesma medida do antigo segmento AM. Assim, ND = NA e MD = AM.
Portanto, CN = ND (CND é isósceles) e MD = MB (DMB é isósceles).