A média aritmética é dividida em dois casos: simples e ponderada. Cada uma deles possui uma fórmula para realizarmos seu cálculo. A média aritmética simples é a soma de todos os elementos dividida pela quantidade deles; já a média aritmética ponderada é a soma do produto de cada elemento pelo seu peso, dividida pela soma dos pesos.
Calcular a média dá-nos um valor central que representa todo aquele conjunto. Trabalha-se com média, por exemplo, para tomar-se decisões na estatística.
Leia também: Probabilidade – estimativa da chance de um determinado evento ocorrer
A média arimética simples é a mais comum, sendo utilizada muitas vezes na escola, para calcular-se a média anual de um aluno, ou nas contas de energia e água, para calcular-se o consumo médio anual ou até mesmo o valor médio pago mensalmente.
É dada pela soma de todos os seus elementos dividida pela quantidade deles. O símbolo de média é o x com um traço em cima, por exemplo, a média entre x1, x2, x3, … xn é calculada pela fórmula:
![]()
n → quantidade de elementos
Para calcular a média simples pela fórmula, basta conhecermos os seus elementos e sabermos o valor de n, ou seja, a quantidade deles.
Exemplo: As temperaturas máximas na cidade de Goiânia foram mensuradas e anotadas durante uma semana do mês de junho conforme a lista seguinte:
Domingo → 28 ºC
Segunda-feira → 30 ºC
Terça-feira → 29 ºC
Quarta-feira → 31 ºC
Quinta-feira → 32 ºC
Sexta-feira → 33 ºC
Sábado → 34 ºC
Vamos determinar a temperatura máxima média dessa semana, para isso sabemos que há 7 dias semanais, então, a média aritmética simples será calculada pela soma das 7 temperaturas divida por 7.
n = 7

Isso que significa que o valor da temperatura máxima da cidade de Goiânia é, em média, 31 ºC.
A média arimética ponderada exige um pouco mais de atenção durante o seu cálculo. Acontece que há valores que possuem maior importância, logo, vamos atribuir a eles fatores de ponderação conhecidos como peso. Quanto maior o valor desse peso, maior a sua influência sobre o valor da média.
Por exemplo, em uma escola, o professor avalia os alunos com 4 critérios: participação, prova escrita, trabalho em grupo e atividades do caderno. Nessa avaliação, o professor atribui os seguintes pesos:
Participação → peso 1
Atividades do caderno → peso 2
Prova escrita → peso 3
Trabalho em grupo → peso 4
Analisando esses pesos, percebe-se que a nota que o aluno tirar em um trabalho em grupo vai afetar muito mais a sua média do que a nota tirada em participação, já que o peso do trabalho em grupo é maior.
Se a um determinado conjunto de valores — x1, x2, x3, … xn — forem atribuídos pesos p1, p2, p3 … pn, respectivamente, a média aritmética ponderada será calculada pela soma das notas (multiplicadas uma a uma pelos seus pesos) dividida pela soma dos pesos.
![]()
Veja também: Progressão aritmética – sequência numérica que segue determinada razão
Para calcular a média ponderada, multiplica-se cada um dos valores pelo seu peso, depois, realiza-se a adição desses resultados, essa soma será dividida pela soma dos pesos, veja o exemplo:
Utilizando a mesma situação da escola, atribui-se os seguintes pesos:
Participação → peso 1
Atividades do caderno → peso 2
Prova escrita → peso 3
Trabalho em grupo → peso 4
A aluna Amanda e o aluno Bernardo decidiram calcular as suas médias para saber quem tirou a melhor nota.
|
Critério/aluno |
Amanda |
Bernardo |
|
Participação |
10 |
6 |
|
Atividades do caderno |
9 |
7 |
|
Prova escrita |
8 |
8 |
|
Trabalho em grupo |
7 |
10 |
Vamos calcular a média da Amanda:
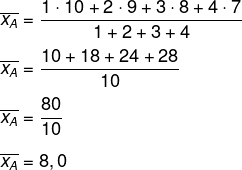
Agora calcularemos a média de Bernardo:
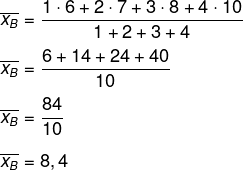
A média de Bernardo é maior do que a média da Amanda.
Para saber melhor como ocorre o cálculo desse tipo específico de média aritmética, leia: Média ponderada.

Questão 1 - (Enem) A Comissão Interna de Prevenção de Acidentes (CIPA) de uma empresa, observando os altos custos com os frequentes acidentes de trabalho ocorridos, fez, a pedido da diretoria, uma pesquisa do número de acidentes sofridos por funcionários. Essa pesquisa, realizada com uma amostra de 100 funcionários, norteará as ações da empresa na política de segurança no trabalho.
Os resultados obtidos estão no quadro.

A média do número de acidentes por funcionário na amostra que a CIPA apresentará à diretoria da empresa é:
a) 0,15
b) 0,30
c) 0,50
d) 1,11
e) 2,22
Resolução
Alternativa D.
Analisando a tabela, faremos o cálculo de uma média ponderada, em que o peso é a quantidade de trabalhadores, que sabemos ser igual a 100.

Questão 2 – Durante a pandemia do coronavírus em 2020, foi declarado que o isolamento social é a melhor alternativa para retardar a propagação da doença. Sendo assim, a empresa de energia informou que não faria mais medições do consumo e que o valor da conta nesse período seria calculado pela média do valor pago pelas 6 últimas faturas.
Kárita é uma pessoa bastante precavida e, para não ter uma surpresa com a chegada das contas, resolveu antecipar-se calculando a média dos 6 meses anteriores para prever qual será o valor da próxima fatura. Sabendo que os valores das 6 últimas faturas são estes:
1 - R$ 150
2 - R$ 120,50
3 - R$ 151,25
4 - R$ 163,15
5 - R$ 142,10
6 - R$ 130
Qual será o valor pago por ela na próxima conta?
a) R$ 143
b) R$ 144
c) R$ 145
d) R$ 146
e) R$ 150
Resolução
Alternativa A.
Calculando a média aritmética, temos:
