Clique e aprenda a fazer o estudo dos sinais de uma função do segundo grau a partir de suas raízes e concavidade.
Uma função do segundo grau é uma regra que relaciona cada elemento de um conjunto a um único elemento de outro e que pode ser reduzida à forma: f(x) = ax2 + bx + c. O estudo dos sinais de uma função do segundo grau é uma análise que determina os intervalos de números reais nos quais a função é positiva, negativa ou nula.
Ideia central do estudo dos sinais
Ao fazer o estudo dos sinais de uma função do segundo grau, estamos interessados em descobrir:
quais são os números x pertencentes ao domínio dessa função que fazem com que a sua imagem y seja positiva;
quais os valores de x fazem com que y seja negativo;
e quais valores de x fazem com que y seja nulo.
Graficamente, estamos procurando os intervalos no eixo 0x onde a função está acima do eixo x, abaixo do eixo x e sobre o eixo x. Isso significa que estamos buscando os respectivos intervalos em que a função é positiva, negativa ou nula.
Observe o gráfico da função do segundo grau f(x) = x2 – 4x + 3:
No gráfico acima, para todos os valores de x maiores do que 1 e, ao mesmo tempo, menores do que 3, a função está abaixo do eixo x. Logo, os valores de y são negativos. Observe também que a função está acima do eixo x para todos os valores de x maiores do que 3 e menores do que 1. Dessa forma, a função é positiva nesses dois intervalos. A função é nula nos pontos de encontro entre ela e o eixo x, portanto, nesse caso, exatamente sobre os pontos 1 e 3 do eixo x.
Essa análise pode ser usada sempre que o gráfico da função estiver disponível. Quando ele não estiver, pode-se usar o método algébrico, que descrevemos abaixo, ou construir o gráfico da função.
Método algébrico
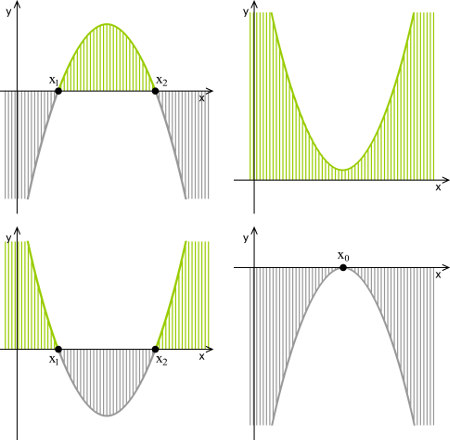
É possível realizar o estudo dos sinais de uma função do segundo grau a partir de suas raízes. Assim, analisa-se, por elas, a concavidade da parábola que representa a função. Para isso, é necessário encontrar as raízes da função do segundo grau, por qualquer método, e determinar a concavidade da parábola que representa essa função. Isso pode ser feito observando o coeficiente a:
Se a > 0, a concavidade da parábola está voltada para cima.
Se a parábola está voltada para baixo.
Em uma dada função do segundo grau f(x) = ax2 + bx + c, suponha que suas raízes sejam x1 e x2.
Se o coeficiente a > 0, a concavidade da parábola está voltada para cima. Para essa função, o intervalo ]x1, x2[ faz com que a função seja negativa; os valores maiores que x2 e menores que x1 fazem com que a função seja positiva, se x2 > x1. Além disso, os próprios valores de x1 e x2 são os pontos onde a função é nula.
Se o coeficiente a parábola é voltada para baixo. Assim, o intervalo ]x1, x2[ faz com que a função seja positiva; os valores maiores que x2 e menores que x1 fazem com que a função seja negativa, se x2 > x1. Além disso, os próprios valores de x1 e x2 são os pontos onde a função é nula.
Exemplo:
Dada a função f(x) = x2 – 4x, suas raízes são:
x2 – 4x = 0
x(x – 4) = 0
x = 0 ou
x – 4 = 0
x = 4
Como a = 1 > 0, então, no intervalo entre 0 e 4, a função é negativa. Para qualquer valor maior que 4, ou menor que 0, a função é positiva; e sobre os pontos 0 e 4, essa função é nula.