Circunferência é uma figura plana construída pelo conjunto de pontos que estão a uma mesma distância do centro. Conhecidos como elementos da circunferência, chamamos de centro ou origem o ponto que está no centro; de raio, o segmento de reta que liga o centro até a circunferência; de corda, qualquer seguimento que liga duas extremidades da circunferência; e de diâmetro, qualquer corda que passa pelo centro. O comprimento e a área da circunferência são calculados por fórmulas específicas.
Veja também: Triângulo retângulo – figura plana que apresenta entre seus três ângulos um de 90º
Para construirmos uma circunferência, precisamos de um ponto conhecido como centro ou origem e de uma distância determinada conhecida como raio. A circunferência é formada por todos os pontos que estão a uma mesma distância r do centro. Note que o centro não faz parte da circunferência, mas é a referência para sua construção.
Entendendo bem a construção da circunferência, podemos definir seus elementos, que são o centro, o raio, a corda e o diâmetro.
Centro e raio: fundamental para a construção da circunferência, como o nome sugere, centro é um ponto que está a uma mesma distância da circunferência. Já o raio, denotado por r, é qualquer seguimento de reta que parte do centro e vai até a circunferência. A distância r é de grande importância para calcular-se a área e o comprimento dessa figura.

C → centro
r → raio
Corda e diâmetro: corda é qualquer segmento de reta que possui as duas extremidades na circunferência. Já o diâmetro é uma corda que passa pelo centro da circunferência, sendo a maior corda dessa figura.
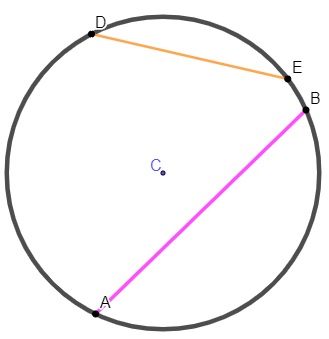

O comprimento do diâmetro é sempre igual ao dobro do raio.
|
d = 2r |
Muitos acham que circunferência e círculo são a mesma coisa, porém não é bem assim. Como vimos, circunferência é o conjunto de pontos que estão a uma mesma distância do centro, já o círculo é a região delimitada pela circunferência. De forma direta, circunferência é o “contorno”, e círculo é a região interna da figura.

Veja também: Diferença entre circunferência, círculo e esfera
Trata-se da mesma ideia de quando se calcula o perímetro de um polígono. O comprimento da circunferência é calculado por:
|
C = 2·π·r |
C → comprimento
r → raio
π → (lê-se: pi)
O π é uma letra grega que utilizamos para representar uma constante, sendo útil para cálculos com a circunferência. Como o π é um número irracional (π = 3,141592653589793238...), para fazer as contas, realizamos uma aproximação dele.
Em questões de vestibulares, Enem e concurso, esse valor é dado no enunciado, o mais adotado é o de 3,14, porém há questões que usam 3,1 ou até mesmo 3 como valor de π.
Exemplo
Calcule o comprimento da circunferência que possui raio igual a 4 cm (use π = 3,1):
C = 2 π r
C = 2 · 3,1 · 4
C = 6,2 · 4
C = 24,8 cm
Exemplo 2
Calcule o comprimento da circunferência a seguir sabendo que o seu diâmetro é dado em cm.
(Use π = 3,14)
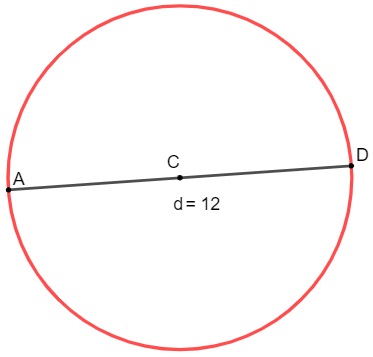
Sendo d = 12 cm, então o raio é a metade do diâmetro, r = 6.
C = 2 π r
C = 2 · 3,14 · 6
C = 6,28 · 6
C = 37,68 cm
A área de um círculo é calculada utilizando-se a fórmula:
|
A= π·r² |
A → área
r → raio
π → (lê-se: pi)
Exemplo
Qual é a área do círculo da imagem a seguir? (π = 3)
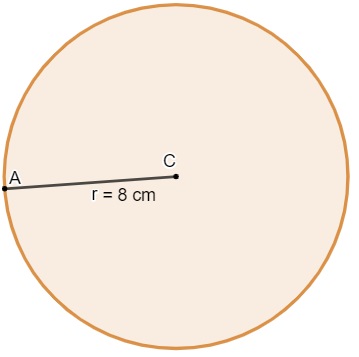
r = 8 e π = 3
A = π · r²
A = 3 · 8²
A = 3 · 64
A = 192 cm²
Exemplo 2
Calcule a área de um círculo delimitado por uma circunferência de diâmetro igual a 10 cm.
Se o diâmetro é 10 cm, o raio será 5 cm.
Como a questão não nos deu valor para π, não substituiremos nenhum valor no lugar dele.
A = π · r²
A = π · 5²
A = 25 π cm²
Veja também: Cone – sólido geométrico cuja base é formada por uma circunferência

Questão 1 - Um ciclista está percorrendo uma praça no formato circular com 15 m de diâmetro. Sabendo-se que, ao final do treino, ele completou 150 voltas, a quantidade de km percorrida foi de: (Use π = 3)
a) 13,5 km
b) 135 km
c) 22,5 km
d) 250 km
Resolução
Alternativa A.
1º passo: calcular o comprimento da circunferência:
C = 2 π r
C = 2 · 3 · 15
C = 6 · 15
C = 90 m
2º passo: multiplicar o último resultado pela quantidade de voltas dadas:
90 · 150 = 13.500 m
3º passo: converter metros para quilômetros (basta dividir por 1000)
13.500 : 1000 = 13,5 km
Questão 2 - A tampa de uma bueiro quebrou, e foi necessário confeccionar outra. Para que ela fique perfeita, ela precisa ter a mesma área da tampa anterior. Para isso, a empresa de saneamento fez a medida do raio da tampa anterior conforme a figura a seguir:
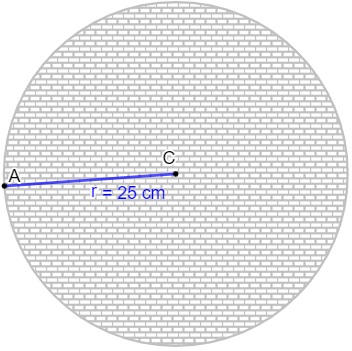
A área da tampa é igual a:
(Use π = 3,14)
a) 780,5 cm²
b) 1875 cm²
c) 625 cm²
d) 1962,5 cm²
Resolução
Alternativa D.
A = π · r²
A = 3,14 · 25²
A = 3,14 · 625
A = 1962,5 cm²