Semelhança de triângulos

Ao comparar duas figuras, geométricas ou não, é possível concluir se elas são iguais, congruentes, semelhantes ou diferentes. Para afirmar que duas figuras são semelhantes é preciso, após compará-las, concluir que elas possuem características parecidas, mas não são iguais. No caso da geometria, polígonos são considerados semelhantes quando eles possuem ângulos correspondentes com medidas congruentes e lados correspondentes proporcionais.

Ângulos congruentes são aqueles cujas medidas são iguais, mas estão em figuras diferentes. Pode-se afirmar que eles tem “o mesmo tamanho”, mas não é possível dizer que trata-se do mesmo ângulo.

Para que lados correspondentes sejam proporcionais, é necessário dividir as medidas de dois lados de uma figura pelas medidas de outros dois lados correspondentes da segunda figura. Se o resultado dessas divisões for igual, então dizemos que esses lados são proporcionais.

No caso dos triângulos, a regra é a mesma, mas existem alguns casos de congruência de triângulos em que é possível verificar se os triângulos são congruentes sem ter que observar todos os seus lados e ângulos.

1- Caso de semelhança ângulo – ângulo (AA). No primeiro desses casos, procure por dois ângulos iguais entre os triângulos comparados.

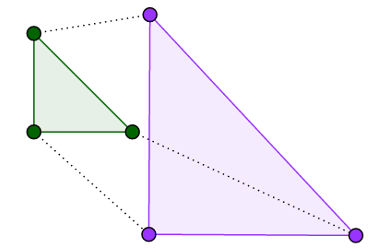
Nos triângulos acima é possível encontrar dois ângulos iguais, portanto, sem a necessidade de medir o terceiro ângulo ou os lados, podemos concluir que esses triângulos são semelhantes.

2- Caso de semelhança Lado – Lado – lado (LLL). No segundo caso, procure dividir os lados de um triângulo pelos lados correspondentes do segundo triângulo. Se o resultado dessas divisões for igual, então os triângulos são semelhantes

Nos triângulos acima é possível encontrar 3 lados correspondentes proporcionais:

AC = BC = BA = 2
DE    EF    FD      

Portanto, sem a necessidade de medir qualquer ângulo, podemos dizer que eles são semelhantes.

3- Caso de semelhança Lado – ângulo – Lado (LAL). No terceiro caso, verifique se dois lados dos triângulos comparados são proporcionais e, logo após, compare o ângulo que fica entre esses lados. Se os lados forem proporcionais e os ângulos forem congruentes, então os triângulos são semelhantes.

Nos triângulos acima é possível notar que:

DE = FD = 2
AC    BA       

Além disso, os ângulos que ficam justamente entre os segmentos observados têm a mesma medida. Desta forma, configura-se o caso LAL.

Por Luiz Paulo Moreira
Graduado em Matemática

Aproveite para conferir nossas videoaulas sobre o assunto: