Prova real é um procedimento utilizado para analisar se o resultado de um cálculo com uma das operações matemáticas está correto ou incorreto.
Prova real é um processo envolvendo as operações matemáticas usado para avaliar se um resultado está correto ou incorreto. Na imagem acima, por exemplo, temos um cálculo de adição: 2 + 3 = 5. Esse resultado está correto?
Observe que partimos de 2, adicionamos 3 e obtivemos 5. O inverso de adicionar 3 é subtrair 3. Assim, se o resultado da primeira operação realmente for 5, ao partirmos de 5 e subtrairmos 3, devemos obter 2, do qual partimos no primeiro cálculo. Como o resultado de 5 – 3 é 2, concluímos que a primeira operação 2 + 3 = 5 está correta.
Leia também: Tabuada — tabela que organiza visualmente as operações matemáticas básicas
A prova real é um método de verificação de cálculos envolvendo as operações matemáticas. Essa técnica se baseia no conhecimento da estrutura de cada operação e no uso da operação inversa. Nesse texto, vamos falar sobre as provas reais das quatro operações básicas: adição, subtração, multiplicação e divisão.
Para fazer a prova real de uma operação, é necessário reconhecer a operação inversa. Duas operações são inversas quando têm funcionamentos contrários, ou seja, uma faz e a outra desfaz (utilizando o resultado da primeira operação como ponto de partida).
Não se preocupe se parecer confuso neste primeiro momento, continue a leitura e observe atentamente os exemplos para cada operação.
Para fazer a prova real de uma operação de adição, precisamos descobrir qual é sua operação inversa. O inverso de adicionar é subtrair, assim, a operação inversa da adição é a subtração. Em um cálculo de adição, partimos de uma parcela e adicionamos a outra, obtendo o resultado (chamado de soma):
parcela 1 + parcela 2 = soma
A prova real da adição é fazer a subtração entre a soma e a parcela 2 e verificar se obtemos novamente a parcela 1:
soma – parcela 2 = parcela 1
Carlos fez a operação 11 + 17 e obteve 28 como resultado. Faça a prova real e justifique se o resultado de Carlos está correto ou incorreto.
Resolução:
Se 11 + 17 for igual a 28, então 28 – 17 deve ser igual a 11. Fazendo a prova real, temos:
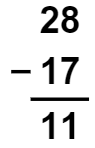
A partir da prova real, concluímos que o resultado de João está correto.
Da mesma forma que a operação inversa da adição é a subtração, a operação inversa da subtração é a adição. Em um cálculo usando a operação da subtração, partimos de uma parcela e subtraímos a outra, obtendo o resultado (chamado de diferença):
parcela 1 – parcela 2 = diferença
A prova real da subtração é fazer a adição entre a diferença e a parcela 2 e verificar se obtemos novamente a parcela 1:
diferença + parcela 2 = parcela 1
Miriam fez a operação 77 – 31 e obteve 56 como resultado. Faça a prova real e justifique se o resultado de Miriam está correto ou incorreto.
Resolução:
Se 77 – 31 for igual a 56, então 56 + 31 deve ser igual a 77. Fazendo a prova real, temos:
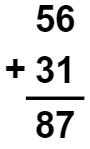
Com base na prova real, concluímos que o resultado de Miriam está incorreto.
Como temos visto até aqui, para fazer a prova real de uma operação de multiplicação, precisamos descobrir qual é sua operação inversa. Assim, a operação inversa da multiplicação é a divisão. Em um cálculo de multiplicação, partimos de um fator e multiplicamos pelo outro, obtendo o resultado (chamado de produto):
fator 1 ×
fator 2 = produto
A prova real da multiplicação é fazer a divisão entre o produto e o fator 2 e verificar se obtemos novamente o fator 1:
produto ÷ fator 2 = fator 1
Carlos fez a operação 7 × 9 e obteve 54 como resultado. Faça a prova real e justifique se o resultado de Carlos está correto ou incorreto.
Resolução:
Se 7 × 9 for igual a 54, então 54 ÷ 9 deve ser igual a 7. Fazendo a prova real, temos:
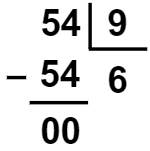
Com base na prova real, concluímos que o resultado de Carlos está incorreto.
Da mesma forma que a operação inversa da multiplicação é a divisão, a operação inversa da divisão é a multiplicação. Entre as quatro operações, a operação da divisão é a mais complexa. Por causa disso, a prova real da divisão é uma das mais úteis. Em um cálculo de divisão, partimos de um número (dividendo) e dividimos por outro (divisor), obtendo o resultado (chamado de quociente) e o resto.
Isso significa que a própria estrutura do algoritmo da divisão já apresenta uma multiplicação entre o divisor e o quociente:
dividendo = (quociente × divisor) + resto
Vamos analisar um exemplo.
Laís fez a operação 102 ÷ 3 e obteve 34 como resultado e resto 0. Faça a prova real e justifique se o resultado de Laís está correto ou incorreto.
Resolução:
Se 102 ÷ 3 resultar em um quociente 34 e resto 0, então 34×3+0
deve ser igual a 102. Fazendo a prova real, temos:
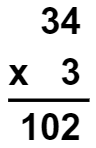
Com base na prova real, concluímos que o resultado de Laís está correto.
Acesse também: Como funciona o algoritmo da divisão?
Questão 1
A diferença entre um número X e 105 é igual a 451. Quanto vale X?
A) 520
B) 556
C) 601
D) 646
Resolução:
Alternativa B
Se X – 105 é igual a 451, então 451 + 105 é igual a X, pois a adição é a operação inversa da subtração. Assim, X = 451 + 105 = 556.
Questão 2
A divisão entre um número Y e 40 é igual ao quociente 175 e resto 0. Quanto vale Y?
A) 1750
B) 2150
C) 4000
D) 7000
Resolução
Alternativa D
Y é igual à multiplicação entre 175 e 40 mais o resto 0, assim, X = 175 × 40 = 7000.
Fontes
ALENCAR, E. S. Os saberes docentes sobre o objeto matemático da divisão. Revista BOEM, Florianópolis, 2013. Disponível em: https://www.revistas.udesc.br/index.php/boem/article/view/3972.
NOGUEIRA, C. M. I.; SIGNORINI, M. B. Crianças, algoritmos e o sistema de numeração decimal. Investigações em Ensino de Ciências, [S. l.], 2016. Disponível em: https://ienci.if.ufrgs.br/index.php/ienci/article/view/295.