Equações do segundo grau

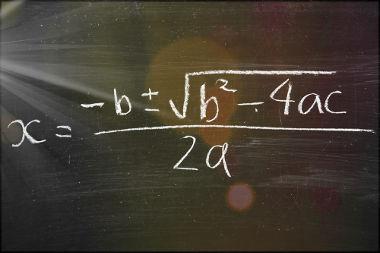
Toda equação que puder ser escrita na forma ax² + bx + c = 0 será chamada equação do segundo grau. O único detalhe é que a, b e c devem ser números reais, e a não pode ser igual a zero em hipótese alguma.

Uma equação é uma expressão que relaciona números conhecidos (chamados coeficientes) a números desconhecidos (chamados incógnitas), por meio de uma igualdade. Resolver uma equação é usar as propriedades dessa igualdade para descobrir o valor numérico desses números desconhecidos. Como eles são representados pela letra x, podemos dizer que resolver uma equação é encontrar os valores que x pode assumir, fazendo com que a igualdade seja verdadeira.

Nas equações do segundo grau, a técnica mais conhecida para encontrar os valores de x, também chamados resultados, raízes ou zeros, é a fórmula de Bháskara.

Essa fórmula será discutida em passos, nos quais geralmente ela é separada em partes para facilitar seu ensino e compreensão.

1 – Determinar os coeficientes da equação

Os coeficientes de uma equação são todos os números que não são a incógnita dessa equação, sejam eles conhecidos ou não. Para isso, é mais fácil comparar a equação dada com a forma geral das equações do segundo grau, que é: ax² + bx + c = 0. Observe que o coeficiente "a" multiplica x², o coeficiente "b" multiplica x, e o coeficiente “c” é constante.

Por exemplo, na seguinte equação:

x² + 3x + 9 = 0

O coeficiente a = 1, o coeficiente b = 3 e o coeficiente c = 9.

Na equação:

– x² + x = 0

O coeficiente a = – 1, o coeficiente b = 1 e o coeficiente c = 0.

2 – Encontrar o discriminante

O discriminante de uma equação do segundo grau é representado pela letra grega  e pode ser encontrado pela seguinte fórmula:

Δ = b² – 4·a·c

Nessa fórmula, a, b e c são os coeficientes da equação do segundo grau. Na equação: 4x² – 4x – 24 = 0, por exemplo, os coeficientes são: a = 4, b = – 4 e c = – 24. Substituindo esses números na fórmula do discriminante, teremos:

Δ = b² – 4·a·c

Δ= (– 4)² – 4·4·(– 24)

Δ = 16 – 16·(– 24)

Δ = 16 + 384

Δ  = 400

3 – Encontrar as soluções da equação

Para encontrar as soluções de uma equação do segundo grau usando fórmula de Bháskara, basta substituir coeficientes e discriminante na seguinte expressão:

x = – b ± √Δ
        2·a

Observe a presença de um sinal ± na fórmula de Bháskara. Esse sinal indica que deveremos fazer um cálculo para √Δ positivo e outro para √Δ negativo. Ainda no exemplo 4x² – 4x – 24 = 0, substituiremos seus coeficientes e seu discriminante na fórmula de Bháskara:

x = – b ± √Δ
        2·a

x = – (– 4) ± 400
        2·4

x = 4 ± 20
      8
 

x = 4 + 20 = 24 = 3
    8         8

x= 4 – 20 = –16 = –2
  8          8

Então, as soluções dessa equação são 3 e – 2, e seu conjunto de solução é:

S = {3, – 2}

Aproveite para conferir nossa videoaula relacionada ao assunto: