Resolver um sistema de equações significa determinar valores para as incógnitas que satisfaçam todas as equações do sistema.
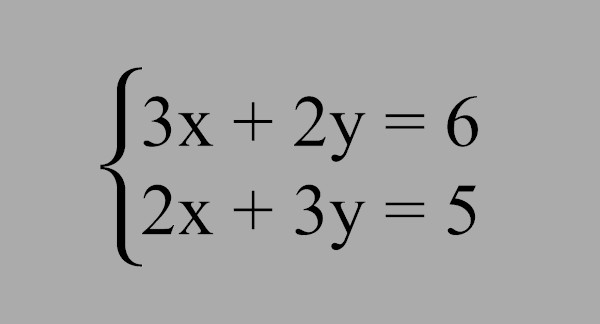
Sistema de equações é um agrupamento simultâneo de equações. A solução de um sistema é um conjunto de valores para as incógnitas que satisfaçam, ao mesmo tempo, todas as equações. Assim, para resolver um sistema, é necessário trabalhar as equações em conjunto.
Leia também: Como resolver equações do 1º grau
A descrição matemática de um fenômeno ou situação pode envolver duas ou mais equações simultaneamente. Esse grupo de equações é chamado de sistema de equações.
Neste texto vamos considerar sistemas lineares, cujas equações são escritas no seguinte formato:
\(a_1x_1+a_2x_2+\ldots+a_nx_n=k\)
Em que \(\left(a_1,a_2,\ldots,a_n\right)\) são coeficientes, \(\left(x_1,x_2,\ldots,x_n\right)\) são incógnitas, e k é o termo independente.
São exemplos de sistemas de equações:
Para resolver um sistema de equações, devemos determinar quais valores para as incógnitas satisfazem, ao mesmo tempo, todas as equações. Vejamos dois métodos para a resolução de um sistema de equações. É possível utilizá-los em etapas distintas.
O método da substituição consiste em isolar uma das incógnitas em uma das equações e substituir a expressão correspondente em outra equação, de modo a construir equações que envolvam quantidades menores de incógnitas.
Exemplo: Em uma escola, a diferença entre o número de alunos e professores é, nessa ordem, 580, e a soma é 620. Quantos alunos e quantos professores há nessa escola?
Seja x o número de alunos e y o número de professores. Assim, temos o seguinte sistema:
\( \begin{cases} x-y=580 \quad \\ x+y=620 & \quad \end{cases}\)
Vamos aplicar o método da substituição.
Primeiro, escolheremos uma das equações e isolaremos uma das incógnitas dessa equação. Escolheremos, por exemplo, a primeira equação e a incógnita x. Assim, isolando x na primeira equação, temos:
\(x=580+y\)
Agora, vamos substituir essa expressão para x na segunda equação:
\(\left(580+y\right)+y=620\)
Observe que reescrevemos a segunda equação do sistema de modo a envolver apenas a incógnita y. Consequentemente, podemos determinar o valor dessa incógnita:
\(2y=620-580\)
\(y=20\)
Sabendo o valor de y, podemos substituir em qualquer uma das equações do sistema original para encontrar o valor de x. Vamos escolher, por exemplo, a primeira equação:
\(x-20=580\)
\(x=600\)
Desse modo, a solução desse sistema é 600, 20, ou seja, há 600 alunos nessa escola e 20 professores.
Para conferir mais exemplos da utilização desse método, clique aqui.
O método da adição consiste em adicionar duas equações de modo que a soma elimine uma das incógnitas. Em muitos casos, para aplicar esse método, é necessário multiplicar uma das equações por um valor conveniente de forma a obter termos que se cancelam.
Exemplo: Determine a solução do seguinte sistema:
\( \begin{cases} y+z=7 \quad \\ 3y+z=15 & \quad \end{cases}\)
Observe que tanto na primeira quanto na segunda equação há o termo +z. Se em uma delas houvesse, ao invés disso, o termo -z, a adição das duas equações eliminaria a incógnita z .
Para que isso ocorra, multiplicaremos a segunda equação por -1. Assim, obteremos o seguinte sistema, equivalente ao original (ou seja, possui a mesma solução):
\( \begin{cases} y+z=7 \quad \\ -3y-z=-15 & \quad \end{cases}\)
Agora vamos adicionar as duas equações:
\(\left(y+z\right)+\left(-3y-z\right)=7+\left(-15\right)\)
\(y-3y+z-z=7-15\)
Como +z-z=0 , temos:
\(-2y=-8\)
\(y=4\)
Agora substituiremos o valor de y em qualquer uma das equações. Vamos escolher, por exemplo, a primeira equação:
\(4+z=7\)
\(z=3\)
Assim, a solução do sistema é y=4 e z=3, ou seja, (4,3).
Existem três tipos de sistema de equações lineares:
Até aqui, todos os exemplos trabalhados foram sistemas possíveis e determinados. Vejamos exemplos dos outros tipos de sistemas:
Exemplo SPI:
\( \begin{cases} x+2y=8 \quad \\ 2x+4y=16 & \quad \end{cases}\)
Aplicando o método da substituição, temos que, na primeira equação:
\(x=8-2y\)
Substituindo na segunda equação, temos que:
\(2\cdot\left(8-2y\right)+4y=16\)
\(16-4y+4y=16\)
\(0y=0\)
Observe que há infinitos números reais que podem ser utilizados para y e que satisfazem a expressão 0y=0 .
A conclusão desse raciocínio é que o sistema original possui infinitas soluções. Observe, por exemplo, que 2, 3, 4, 2 e 6, 1 são alguns exemplos de solução desse sistema.
Exemplo SI:
\( \begin{cases} x+y=7 \quad \\ x+y=1 & \quad \end{cases}\)
Note que, pela primeira equação, a soma entre x e y deve ser 7. No entanto, ao mesmo tempo, pela segunda equação, essa soma deve ser 1. Portanto, não há x e y reais que satisfaçam as duas equações concomitantemente, e o sistema não possui solução.
Leia também: Como resolver uma equação do 2º grau
Questão 1
(Enem) Uma barraca de tiro ao alvo de um parque de diversões dará um prêmio de R$ 20 ao participante, cada vez que ele acertar o alvo. Por outro lado, cada vez que ele errar o alvo, deverá pagar R$ 10. Não há cobrança inicial para participar do jogo. Um participante deu 80 tiros e, ao final, recebeu R$100.
Qual foi o número de vezes que esse participante acertou o alvo?
a) 30
b) 36
C) 50
D) 60
E) 64
Resolução
Seja x o número de vezes que o participante acertou o alvo, e y o número de vezes que errou o alvo.
Ao todo, foram 80 tiros. Portanto, x+y=80 .
Ainda, por x acertos, o participante recebeu 20x reais e por y erros perdeu 10y reais (o que vamos representar por -10y). Ao todo, no final do jogo, ele ficou com R$ 100.
Desse modo, o sistema que descreve esse problema é:
\( \begin{cases} x+y=80 \quad \\ 20x-10y=100 & \quad \end{cases}\)
Multiplicando a primeira equação por 10, temos o sistema equivalente:
\( \begin{cases} 10x+10y=800 \quad \\ 20x-10y=100 & \quad \end{cases}\)
Somando as duas equações, obtemos:
\(30x=900\)
\(x=30\)
Alternativa A
Questão 2
(Fuvest) Um supermercado adquiriu detergentes nos aromas limão e coco. A compra foi entregue, embalada em 10 caixas, com 24 frascos em cada caixa.
Sabendo-se que cada caixa continha 2 frascos de detergentes a mais no aroma limão do que no aroma coco, o número de frascos entregues, no aroma limão, foi:
a) 110
b) 120
c) 130
d) 140
e) 150
Resolução
Sejam L e C as quantidades, respectivamente, de detergentes nos aromas de limão e de coco em uma caixa. Portanto, em cada caixa, L+C=24. Ainda, como cada caixa continha 2 frascos de detergentes a mais no aroma limão do que no aroma coco, tem-se L=C+2 .
Logo, o sistema que descreve esse problema é:
\( \begin{cases} L+C=24 \quad \\ L=C+2 & \quad \end{cases}\)
Note que a incógnita L já está isolada na segunda equação. Substituindo a expressão na primeira equação, temos que:
\(\left(C+2\right)+C=24\)
\(2C=22\)
\(C=11\)
Substituindo o valor de C na segunda equação, temos que:
\(L=13\)
Assim, nas 10 caixas entregues, o número de frascos entregues foi de 10⋅13=130 .
Alternativa C
Fontes:
BOLDRINI, J. L. et al. Álgebra Linear. 3ª ed. São Paulo: Harper & Row do Brasil, 1980.
JÚNIOR, J.R.G.; CASTRUCCI, B. A conquista da Matemática: 8° ano. 4 ed. São Paulo: FTD, 2018.
LIMA, Elon L. et al. A Matemática do Ensino Médio: Volume 1. Coleção Professor de Matemática. Rio de Janeiro: SBM, 2016.