Aprenda o que é ponto de máximo e ponto de mínimo e entenda como esses elementos são representados. Esses pontos são definidos de acordo com a maior ou menor coordenada possível de Y e podem representar o ponto mais alto ou mais baixo de uma parábola, que é a figura que representa uma função do segundo grau.
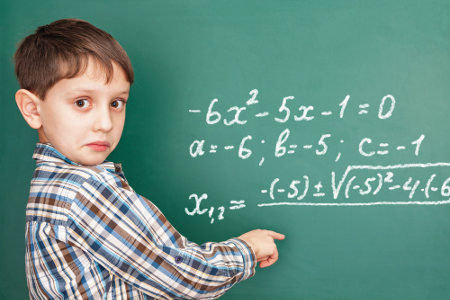
Uma função do segundo grau é uma função que pode ser escrita na forma: f(x) = ax2 + bx + c, em que a ≠ 0. Toda função do segundo grau pode ser representada graficamente por uma parábola. Existem alguns casos em que essa parábola pode estar voltada para cima, possuindo, assim, um ponto de mínimo, e outros em que ela pode estar voltada para baixo, possuindo, assim, um ponto de máximo.
O candidato a ponto de máximo (ou de mínimo) no gráfico de uma parábola é chamado de vértice, portanto, encontrar as coordenadas do vértice equivale a encontrar a localização do ponto de máximo ou de mínimo da parábola. Se V(xv, yv) é o vértice com suas coordenadas, então as fórmulas que podem ser usadas para encontrar essas coordenadas são:
xv = – b
2a
yv = – Δ
4a
Não é necessário construir a parábola para observar seu ponto de máximo. A partir da função do segundo grau, é possível obter todas as informações necessárias algebricamente. Só não é possível ver a localização desse ponto.
Toda parábola/função do segundo grau possui vértice. Esse vértice é o ponto de mínimo se o coeficiente a > 0. Isso faz com que a parábola tenha concavidade voltada para cima e, assim, possua um “valor mínimo”, como mostra a figura a seguir.
Observando o desenho, é possível perceber que “abaixo” do ponto de mínimo não existem outros pontos da parábola. No entanto, o mais correto é dizer que a menor coordenada y de algum ponto pertencente a uma parábola, com a > 0, é a coordenada do ponto de mínimo.
Toda parábola/função do segundo grau com a coordenada a máximo, pois sua concavidade é voltada para baixo e, por isso, ela possui um ponto que é o “mais alto de todos”.
Novamente, o correto é afirmar que não existe nenhum ponto pertencente a essa parábola com coordenada y superior a essa mesma coordenada do vértice.
A imagem a seguir mostra uma parábola com concavidade voltada para baixo e seu ponto de máximo.
É possível determinar se o vértice de uma função é ponto de máximo ou de mínimo apenas conferindo o valor do coeficiente a. Se a > 0, a função possui ponto de mínimo, e se a
Quando a função possui raízes, podemos encontrar as coordenadas do vértice da função da seguinte maneira:
1 – Encontrar as raízes da função.
2 – Encontrar o ponto médio entre as raízes. Esse valor é a coordenada x do vértice.
3 – Encontrar a imagem da função relacionada ao valor encontrado no passo 2 para x do vértice. Esse será o valor de y do vértice.
Determine as coordenadas do vértice da função f(x) = x2 – 16.
Solução 1 – Utilizando as fórmulas
xv = – b
2a
xv = – 0
2·1
xv = 0
2
xv = 0
yv = – Δ
4a
yv = – (b2 – 4ac)
4a
yv = – (0 – 4·1·[– 16])
4
yv = – (– 4·1·[– 16])
4
yv = – (64)
4
yv = – 16
Solução 2 – Encontrando o ponto médio das raízes e a imagem da função relativa a ele
As raízes dessa função podem ser obtidas pela fórmula de Bháskara. Entretanto, usaremos outro método para encontrá-las.
f(x) = x2 – 16
0 = x2 – 16
x2 = 16
√x2 = ± √16
x = ± 4
O ponto médio das raízes é xv:
xv = 4 – 4 = 0 = 0
2 2
Substituindo 0 na função para encontrar yv, teremos:
f(x) = x2 – 16
f(0) = 02 – 16
f(0) = – 16
Portanto, as coordenadas do vértice são: V(0, – 16).