Gráfico da função do segundo grau

Uma função do segundo grau é aquela que pode ser escrita na forma: f(x) = ax² + bx + c. Toda função do segundo grau pode ser representada geometricamente no plano por meio de uma parábola. No caso das funções do primeiro grau, podemos representá-las por retas, e parte do procedimento usado para construí-las também pode ser utilizado na construção das parábolas, embora as figuras sejam muito diferentes.

Gráfico da função do segundo grau

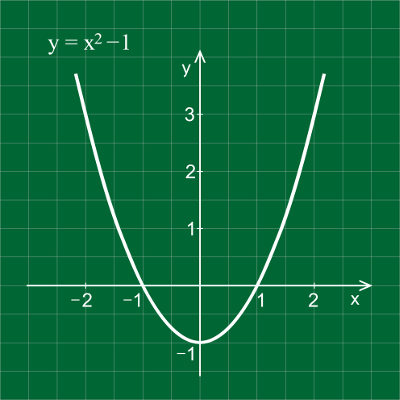
Em primeiro lugar, para construir uma parábola, é necessário possuir alguma referência do formato dessa figura. A imagem a seguir é um exemplo de parábola:

Nas funções do segundo grau, esse gráfico pode ter a concavidade (abertura) voltada para cima ou para baixo.

Dada a função do segundo grau f(x) = x², observe seus valores na tabela a seguir:

 Tabela de valores da parábola

Ao marcar os pares ordenados no plano cartesiano e ligar esses pontos, tendo como base para isso a parábola dada anteriormente, temos a seguinte representação:

Método prático

O método dado anteriormente depende de encontrar o ponto onde a parábola deixa de ser decrescente e passa a ser crescente, ou vice-versa. Devemos, então, encontrar os pontos da parábola que ficam à esquerda desse ponto e outros que ficam à direita.

Para evitar o problema de encontrar esse ponto por tentativa e erro, existe um método prático para encontrar os pontos do gráfico da função do segundo grau que, consequentemente, pode ser usado para fazer essa representação. Esse método será discutido no seguinte passo a passo:

1 – Encontrar as raízes da função

Para encontrar as raízes da função, basta usar a fórmula de Bháskara. Entretanto, mesmo quando a função não possui raízes, podemos construir seu gráfico.

Dadas as raízes x₁ e x₂ de uma função, as coordenadas dessas raízes no plano cartesiano sempre serão: A (x₁, 0) e B (x₁, 0).

2 – Encontrar o vértice

Existem duas formas de encontrar as coordenadas do vértice de uma parábola por meio da função do segundo grau. A primeira é fazer a média dos valores das raízes. O resultado desse cálculo será a coordenada x do vértice. Substituindo essa coordenada na função, encontraremos a coordenada y do vértice.

A segunda maneira de encontrar as coordenadas do vértice de uma parábola, por meio da função do segundo grau, é usando fórmulas. São elas:

x_v = – b
       2a

y_v = – Δ
        4a

As coordenadas do vértice são V (x_v, y_v).

3 – Construir o gráfico

Dados os pontos A, B e V, podemos ligá-los utilizando como base a figura da parábola dada no início do texto. Caso a função não possua raízes, proceda conforme o seguinte passo a passo:

1. Encontre o vértice usando as fórmulas;

2. Escolha um valor para x maior que x_v e um valor para x menor que x_v;

3. Substitua cada um dos valores escolhidos para x na regra da função para descobrir seu respectivo valor de y;

4. Cumprindo os três passos anteriores, teremos três pontos suficientes para construir a parábola.

Exemplo

Construa o gráfico da função f(x) = x² – 4.

1 – Para encontrar as raízes:

Usando a fórmula de Bháskara, encontramos x₁ = 2 e x₂ = – 2, logo, A (2, 0) e B (– 2, 0).

2 – Usando as fórmulas, as coordenadas do vértice são:

x_v = – b
        2a

x_v = – 0
         2

x_v = 0

y_v = – Δ
        4a

y_v = – (b² – 4ac)
             4a    

y_v = – (0² – 4(– 4))
                 4        

y_v = – (16)
            4

y_v = – 4

Portanto, V(0, – 4).

3 – O gráfico, portanto, será:

Aproveite para conferir nossa videoaula relacionadas ao assunto: