A adição é uma das principais operações matemáticas, ela está associada à ideia de juntar ou agrupar elementos de conjuntos. Podemos também, com base nela, definir as operações de subtração e multiplicação. Além disso a operação de adição é bastante utilizada em nosso cotidiano, por exemplo, quando vamos ao supermercado, assim, é muito importante compreender sua ideia e o método de como realizá-la.
Leia também: Sistema de numeração decimal – sistema que utiliza a base 10
A ideia de adição está ligada ao conceito de juntar elementos de dois ou mais conjuntos. Por exemplo, considere o conjunto formado por círculos e o conjunto formado por triângulos.
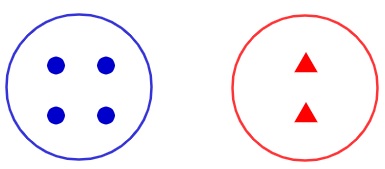
Agora imagine que nosso interesse seja determinar a quantidade total de figuras geométricas, para isso teremos que juntar os círculos com os triângulos. Quando realizamos esse processo, estamos somando a quantidade de círculos com a quantidade de triângulos, e indicamos essa soma com o símbolo +.
Juntando os elementos dos dois conjuntos temos:
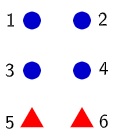
Observe o número de elementos em cada um dos conjuntos, temos 4 (quatro) círculos e 2 (dois) triângulos. Veja também que, ao juntar esses elementos, obtivemos um total de 6 (seis) figuras geométricas, podemos sintetizar todo esse raciocínio em uma expressão matemática, veja:
4 + 2 = 6
Veja que o processo de representar graficamente cada elemento da adição torna-se complicado quando colocamos números maiores. Por exemplo, para determinar a soma de 1500 com 1432, teríamos que desenhar 1500 unidades e, em seguida, 1432 unidades, para, assim, contar a quantidade total delas. Veremos, a seguir, um método que facilita esse processo.
Exemplo 1
Determine a soma entre 1500 e 1432.
Para determinar a soma entre os números, devemos primeiramente “armar” a operação. Esse processo consiste em colocar um número sob o outro de maneira que as unidades do primeiro número fiquem sob as unidades do segundo, assim como as dezenas do primeiro número devem ficar sob as dezenas do segundo, e assim sucessivamente. Veja:
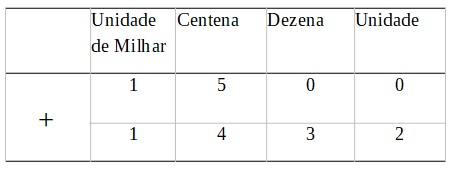
Agora, para determinar o valor da adição, basta somar, termo a termo, os valores da tabela anterior, isto é, somar unidade com unidade, dezena com dezena, e assim por diante.
0 + 2 = 2 → Unidade
0 + 3 = 3 → Dezena
5 + 4 = 9 → Centena
1 +1 = 2 → Unidade de Milhar
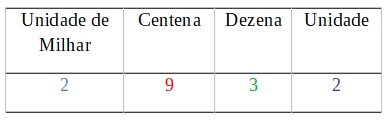
Assim podemos dizer que 1500 + 1432 = 2932. Podemos simplificar a escrita do processo de adição excluindo a tabela e a escrita das ordens, veja:
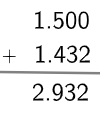
Veja também: Números ordinais – números que representam ordem ou posição
Exemplo 2
Determine a soma entre os números 5854 e 4217.
Novamente o primeiro passo é armar a operação entre os dois números.

Somando então termo a termo temos:
4 + 7 = 11 → Unidades
5 + 1 = 6 → Dezenas
8 + 2 = 10 → Centenas
5 + 4 = 9 → Unidade de Milhar
Ao somar termo a termo, observe que a soma das unidades ultrapassa sua capacidade, assim como a soma das centenas, quando isso ocorre, devemos acrescentar o que foi ultrapassado ao termo da próxima ordem.
Portanto devemos acrescentar 1 dezena à casa das dezenas, retirando-a das unidades, e acrescentar uma 1 unidade de milhar à casa das unidades de milhar, retirando-a da casa das centenas, veja:
4 + 7 = 11 – 10→ Unidades
5 + 1 = 6 + 1 → Dezenas
8 + 2 = 10 – 10→ Centenas
5 + 4 = 9 + 1→ Unidade de Milhar
Logo: 5854 + 4217 = 10.071.
Existe também uma maneira simplificada de realizar esse procedimento, basta subir o número que passa em cada casa para a casa da ordem seguinte, veja:

Exemplo 3
Arme e efetue a adição entre os números 6432 e 9993.

Veja que cada aparição do número 1 em cima dos números 4 e 6 representa, respectivamente, a centena e a unidade de milhar que se ultrapassaram.
Acesse também: Números romanos – sistema de numeração representado por letras
Questão 1 – Arme as seguintes adições e determine seus resultados.
a) 54 + 99
b) 1.544 + 199
c) 77 + 83
d) 1.432.765 + 65.876
e) 87 + 34 + 876
f) 543 + 423 + 54
g) 76 + 43 + 1.677
Resolução
a) 153
b) 1743
c) 160
d) 1.498.641
e) 997
f) 1020
g) 1796
Questão 2 – Preencha com valor correto cada uma das lacunas.
a) 54 + ____ = 67
b) 99 + ____ = 209
c) ____ + 150 = 300
d) ____ + 34 = 100
Resolução
a) 13
b) 110
c) 150
d) 66