União, interseção e diferença são as principais operações entre conjuntos. Para representar visualmente essas operações, utilizamos o diagrama de Venn.
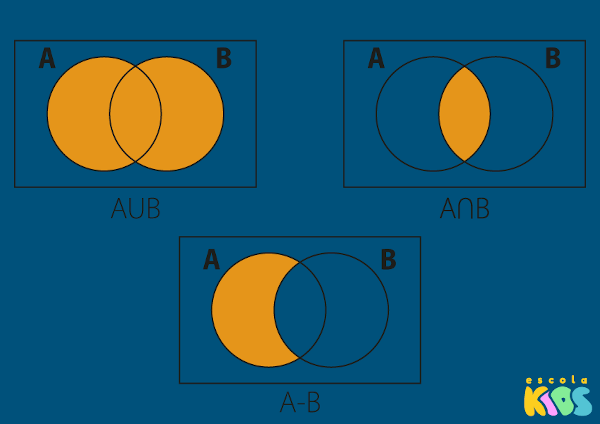
As operações com conjuntos são união, interseção e diferença. O resultado de cada uma dessas operações é um novo conjunto. Para indicar a união entre conjuntos, utilizamos o símbolo ∪; para a interseção, o símbolo ∩; e para a diferença, o símbolo de subtração \(-\). No caso da diferença, é fundamental observar a ordem em que a operação será realizada. Em outras palavras, se A e B são conjuntos, então a diferença entre A e B é diferente da diferença entre B e A.
Leia também: Diagrama de Venn — representação geométrica dos conjuntos e das operações entre eles
As operações com conjuntos são: união, interseção e diferença.
A união (ou reunião) dos conjuntos A e B é o conjunto A ∪ B, formado pelos elementos que pertencem a A ou pertencem a B.
\(A∪B=\{x;x∈A\ ou\ x∈B\}\)
A interseção dos conjuntos A e B é o conjunto A ∩ B, formado pelos elementos que pertencem a A e pertencem a B.
\(A∩B=\{x;x∈A\ e\ x∈B\}\)
A diferença dos conjuntos A e B é o conjunto A – B, formado pelos elementos que pertencem a A e não pertencem a B.
\(A -B =\{x;x∈A\ e\ x ∉B\}\)
Se U (conhecido como conjunto universo) é um conjunto que contém todos os conjuntos de determinado contexto, então a diferença U – A, com A ⊂ U, é chamada de complementar de A. O complementar de A é formado pelos elementos que não pertencem a A e é representado por Ac.
\(A^c=U-A=\{x;x∉A\}\)
As três operações com conjuntos são: união, interseção e diferença.
A união (ou reunião) dos conjuntos A e B é o conjunto A ∪ B (lê-se “A união B”). Este conjunto é formado por todos os elementos que pertencem ao conjunto A ou pertencem ao conjunto B, ou seja, os elementos que pertencem a pelo menos um dos conjuntos.
Representando os elementos de A ∪ B por x, escrevemos
\(A∪B=\{x;x∈A\ ou\ x∈B\}\)
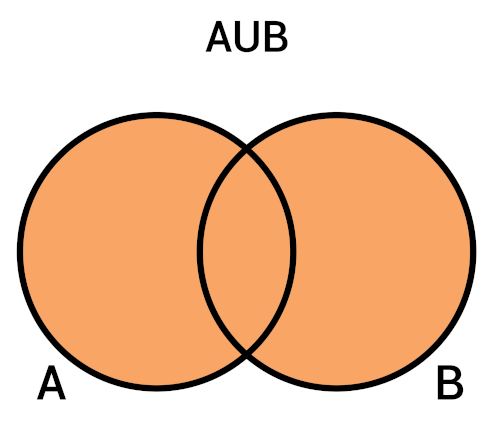
Na imagem abaixo, a região laranja é o conjunto A ∪ B.
Parece difícil? Vejamos dois exemplos!
Exemplo 1:
Qual é o conjunto A ∪ B, se A = {7, 8} e B = {12, 15}?
O conjunto A ∪ B é formado pelos elementos que pertencem a A ou pertencem a B. Como os elementos 7 e 8 pertencem ao conjunto A, então os dois devem pertencer ao conjunto A ∪ B. Ainda, como os elementos 12 e 15 pertencem ao conjunto B, então os dois devem pertencer ao conjunto A ∪ B.
Portanto,
A ∪ B={7, 8, 12, 15}
Note que cada um dos elementos de A∪B pertence ao conjunto A ou ao conjunto B.
Exemplo 2:
Considere os conjuntos A = {2, 5, 9} e B = {1 , 9}. Qual é o conjunto A ∪ B?
Como os elementos 2, 5 e 9 pertencem ao conjunto A, então todos devem pertencer ao conjunto A∪B. Além disso, como os elementos 1 e 9 pertencem ao conjunto B, então todos devem pertencer ao conjunto A ∪ B.
Observe que citamos o 9 duas vezes, pois este elemento pertence ao conjunto A e ao conjunto B. Dizer que “o conjunto A ∪ B é formado pelos elementos que pertencem a A ou pertencem a B” não exclui os elementos que pertencem, simultaneamente, aos conjuntos A e B.
Assim, nesse exemplo, temos que
A ∪ B={1, 2, 5, 9}
Note que escrevemos o elemento 9 apenas uma vez.
A interseção dos conjuntos A e B é o conjunto A ∩ B (lê-se “A interseção B”). Esse conjunto é formado por todos os elementos que pertencem ao conjunto A e pertencem ao conjunto B. Em outras palavras, A ∩ B é composto pelos elementos em comum dos conjuntos A e B.
Indicando os elementos de A ∩ B por x, escrevemos
\(A∩B=\{x;x∈A\ e\ x∈B\}\)
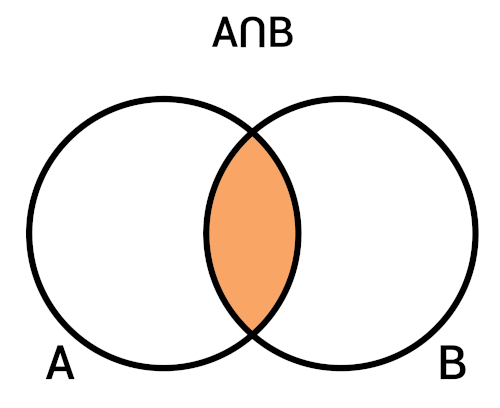
Na imagem abaixo, a região laranja é o conjunto A ∩ B.
Vamos resolver dois exemplos sobre a interseção de conjuntos!
Exemplo 1:
Considere A = {-1, 6, 13} e B = {0, 1, 6, 13}. Qual é o conjunto A ∩ B?
O conjunto A ∩ B é formado por todos os elementos que pertencem ao conjunto A e pertencem ao conjunto B. Observe que os elementos 6 e 13 pertencem, simultaneamente, aos conjuntos A e B.
Assim,
A ∩ B={6, 13}
Exemplo 2:
Qual a interseção entre os conjuntos A = {0,4} e \(B={-3,\frac{1}2,5,16,44}\)?
Perceba que não há nenhum elemento em comum entre os conjuntos A e B. Assim, a interseção é um conjunto sem elementos, ou seja, um conjunto vazio.
Portanto,
\(\)A ∩ B={ } = ∅
A diferença entre os conjuntos A e B é o conjunto A – B (lê-se “diferença entre A e B”). Esse conjunto é constituído por todos os elementos que pertencem ao conjunto A e não pertencem ao conjunto B.
Retratando os elementos de A – B por x, escrevemos
\(A-B=\{x;x∈A\ e\ x∉B\}\)
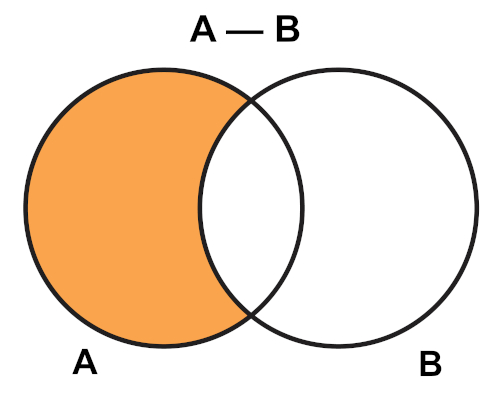
Na imagem abaixo, a região laranja é o conjunto A – B.
Atenção: a diferença entre os conjuntos A e B não é a diferença entre os conjuntos B e A, porque B – A é formado por todos os elementos que pertencem ao conjunto B e não pertencem ao conjunto A.
Considere os dois exemplos adiante sobre diferença entre conjuntos.
Exemplo 1:
Se A = {-7, 2, 100} e B = {2, 50}, então qual é o conjunto A – B? E o conjunto B – A?
O conjunto A-B é formado por todos os elementos que pertencem ao conjunto A e não pertencem ao conjunto B. Observe que 2 é o único elemento do conjunto A que também pertence ao conjunto B. Assim, 2 não pertence ao conjunto A – B.
Portanto,
A – B = {-7, 100}
Ainda, o conjunto B – A é formado por todos os elementos que pertencem ao conjunto B e não pertencem ao conjunto A. Portanto,
B – A = {50}
Exemplo 2:
Qual a diferença entre o conjunto A = {–4, 0} e o conjunto B = {–3}?
Perceba que nenhum dos elementos de A pertence a B. Assim, a diferença A – B é o próprio conjunto A.
\(A - B = \{-4,0\} = A\)
Observação: Considere que U (chamado de conjunto universo) é um conjunto que contém todos os outros conjuntos de determinada situação. Assim, a diferença U – A, com A⊂U, é um conjunto chamado de complementar de A e retratado como \(A_c\).
\(A^c=U-A=\{x; x∉A\}\)
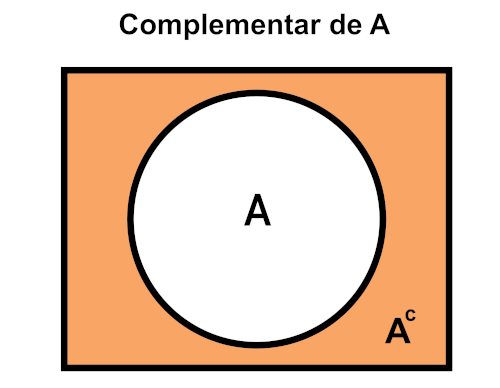
Na imagem a seguir, o retângulo é o conjunto universo e a região laranja é o conjunto \(A_c\).
Saiba mais: Passo a passo de como fazer uma divisão
Questão 1
Considere os conjuntos A = {–12, –5, 3} e B = {–10, 0, 3, 7} e classifique cada afirmação abaixo em V (verdadeira) ou F (falsa).
I. A ∪ B = {–12, –10, –5, 3, 7}
II. A ∩ B = {3}
III. A – B = {–12, –5}
A ordem correta, de cima para baixo, é
A) V-V-V
B) F-V-V
C) V-F-V
D) F-F-V
E) F-F-F
Resolução
I. Falsa.
O elemento 0 deve pertencer à união de A e B, pois 0 ∈ B. Assim, A ∪ B = {–12, –10, –5, 0, 3, 7}
II. Verdadeira.
III. Verdadeira.
Alternativa B.
Questão 2
Considere A = {4, 5}, B = {6,7} e C = {7,8}. Então, o conjunto A ∪ B ∩ C é
A) {7}.
B) {8}.
C) {7, 8}.
D) {6,7,8}.
E) {4, 5, 6, 7, 8}.
Resolução
Observe que A ∪ B = {4, 5, 6, 7}. Portanto, o conjunto A ∪ B ∩ C é a interseção entre A ∪ B = {4, 5, 6, 7} e C = {7,8}. Logo,
A ∪ B ∩ C = {7}
Alternativa A.
Fontes
LIMA, Elon L. Curso de Análise. 7 ed. Rio de Janeiro: IMPA, 1992. v.1.
LIMA, Elon L. et al. A Matemática do Ensino Médio. 11. ed. Coleção Professor de Matemática. Rio de Janeiro: SBM, 2016. v.1.