A esfera é um sólido bastante comum no nosso dia a dia, presente tanto na natureza quanto nas invenções humanas.
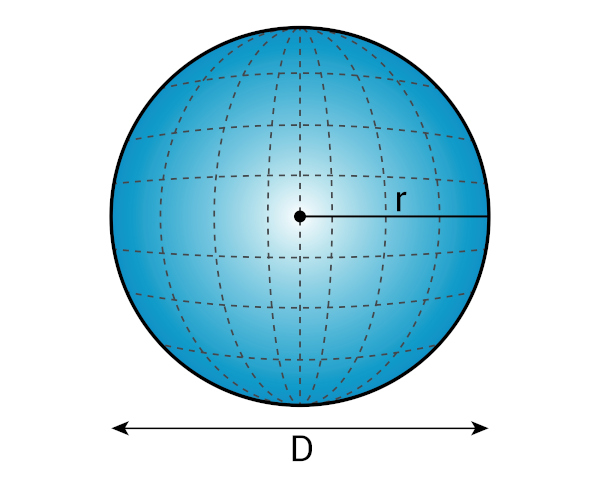
A esfera é um sólido geométrico classificado como corpo redondo devido à sua forma arredondada. Podemos defini-la como o conjunto de pontos no espaço que estão a uma mesma distância do seu centro. Essa distância é um elemento importante da esfera, conhecido como raio.
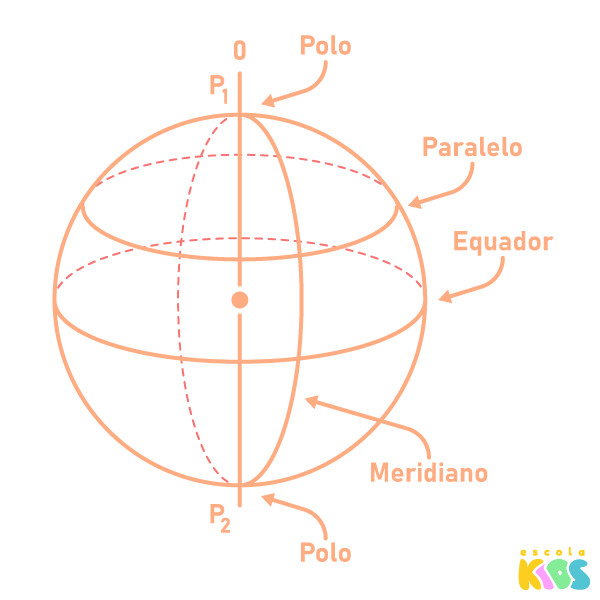
Algumas partes da esfera recebem nomes especiais, como o equador, os polos, os paralelos e os meridianos. Para calcular a área total e o volume da esfera, existem fórmulas específicas.
Leia também: Diferença entre circunferência, círculo e esfera
A esfera é um sólido geométrico classificado como um corpo redondo.
Os principais elementos da esfera são a sua origem e o seu raio.
A área total da esfera é calculada pela fórmula:
\(A=4\pi r^2\)
O volume da esfera é calculado pela fórmula:
\(V=\frac{4}{3}\pi r^3\)
Existem dois elementos fundamentais da esfera, que são o centro e o raio. Quando definimos os definimos, temos que a esfera é o conjunto formado por todos os pontos que estão a uma distância igual ou menor que o comprimento do raio.
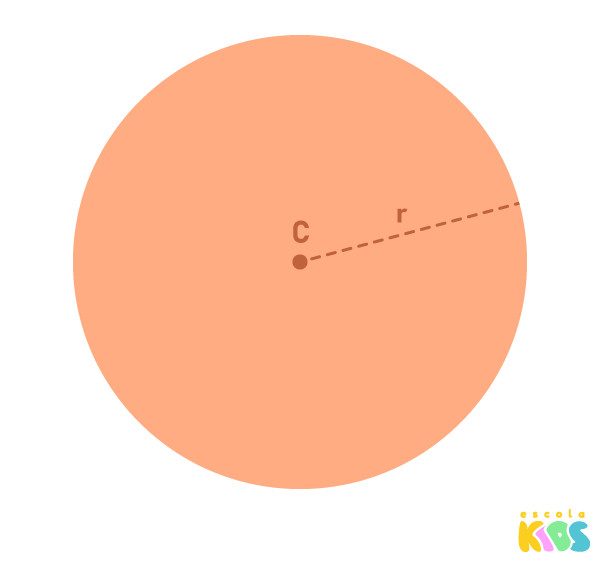
C ➔ centro ou origem da esfera.
r ➔ raio da esfera.
Além dos elementos listados anteriormente, existem outros, que recebem nomes específicos. Há os polos, os meridianos, os paralelos e o equador.
A área de um sólido geométrico é a medida da superfície desse sólido. Podemos calcular a área da esfera por meio da fórmula:
\(A=4\pi r^2\)
Exemplo:
Uma esfera possui raio medindo 12 cm. Utilizando \(\pi=\ 3,14,\) calcule a área dessa esfera.
Resolução:
Calculando a área, temos que:
\(A=4\pi r^2\)
\(A=4\cdot3,14\cdot{12}^2\)
\(A=4\cdot3,14\cdot144\)
\(A=1808,64\ cm²\)
O volume é outra grandeza importante nos sólidos geométricos. Para calcular o volume da esfera, utilizamos a fórmula:
\(V=\frac{4}{3}\pi r^3\)
Logo, basta conhecermos o valor do raio para calcularmos o volume da esfera.
Exemplo:
Uma esfera possui raio medindo 2 metros. Sabendo que \(\pi=3\), calcule o volume dessa esfera.
Resolução:
\(V=\frac{4}{3}\pi r^3\)
\(V=\frac{4}{3}\cdot3\cdot2^3\)
\(V=4\cdot2^3\)
\(V=4\cdot8\)
\(V=32\ m³\)
Existem partes da esfera que recebem nomes específicos, como o fuso esférico, a cunha esférica e o hemisfério.
Fuso esférico: parte da superfície da esfera.
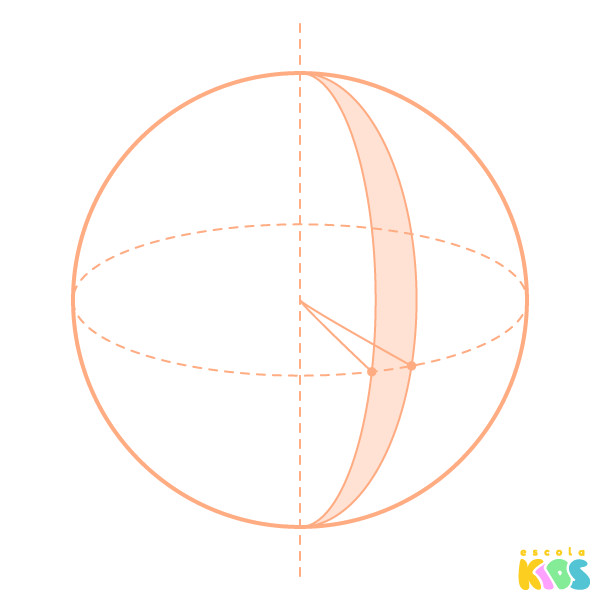
Cunha esférica: sólido geométrico formado pela parte da esfera que vai do fuso à origem, como uma fatia.
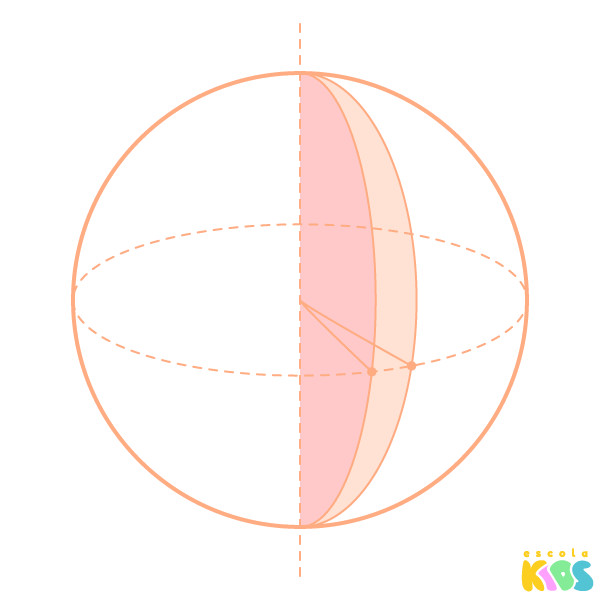
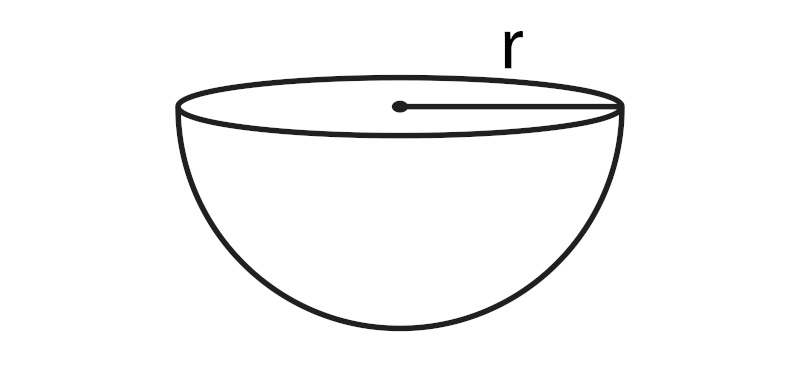
Hemisfério: nada mais é que a metade de uma esfera.
Leia também: Circunferência — figura plana construída pelo conjunto de pontos que estão a uma mesma distância do centro
Questão 1
O pilates é um conjunto de exercícios que auxiliam no desenvolvimento e restauração da saúde. Na prática desses exercícios, é comum o uso de uma bola de ginástica. Em um centro de reabilitação que promove aulas de pilates, uma bola possui 60 cm de diâmetro. Analisando essa bola, podemos afirmar que a área da sua superfície é de:
A) 3600 \(\pi\)
B) 2700 \(\pi\)
C) 2500 \(\pi\)
D) 1700 \(\pi\)
E) 900 \(\pi\)
Resolução:
Alternativa A
Sabemos que a área da superfície é calculada por:
\(A=4\pi r^2\)
Se o diâmetro é de 60 cm, o raio será de 30 cm:
\(A=4\cdot\pi\cdot{30}^2\)
\(A=4\cdot\pi\cdot900\)
\(A=3600\pi cm²\)
Questão 2
Buscando inovar nas embalagens de seus perfumes, uma empresa decidiu desenvolver recipientes que possuem formato de esfera, com raio de 5 cm. Utilizando \(\pi=3\), o volume de um desses recipientes, em cm³, é de:
A) 250 cm³
B) 500 cm³
C) 750 cm³
D) 1000 cm³
Resolução:
Alternativa B
Calculando o volume:
\(V=\frac{4}{3}\pi r^3\)
\(V=\frac{4}{3}\cdot3\cdot5^3\)
\(V=4\ \cdot125\ \)
\(V=500cm^3\)