Ângulos opostos pelo vértice

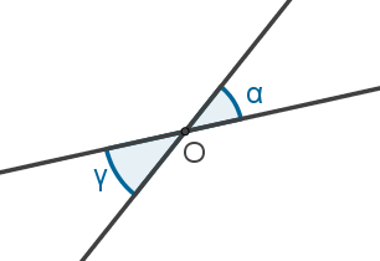
Um ângulo é a medida da abertura entre duas semirretas de mesma origem (mesmo ponto inicial). Observe os quatro ângulos da figura a seguir:

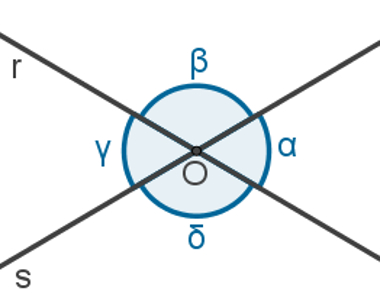
Observe que os ângulos α e β estão sobre a reta r e possuem um lado em comum. Os ângulos γ e β estão sobre a reta s e também possuem um lado em comum. Já os ângulos γ e α não estão sobre a mesma reta, e o único ponto que possuem em comum é o vértice O.

Nesse caso, dizemos que os ângulos α e β são adjacentes, e os ângulos γ e α são opostos pelo vértice. Fazendo uma análise parecida, encontraremos todos os pares de ângulos adjacentes:

α e β

γ e β

γ e δ

δ e α

Os pares de ângulos opostos pelo vértice são os seguintes:

α e γ

β e δ

Propriedades

• Em um cruzamento de duas retas, ângulos adjacentes são suplementares.

Não são quaisquer ângulos adjacentes que são suplementares, somente quando há encontro entre duas retas. Lembrando que ângulos suplementares são aqueles cuja soma é igual a 180°.

Dessa maneira, na figura acima, sempre será verdade que:

α + β = 180°

γ + β = 180°

γ + δ = 180°

δ + α = 180°

• Em um cruzamento de duas retas, ângulos opostos pelo vértice são congruentes.

Lembre-se que dois ângulos são congruentes quando eles são distintos, mas possuem a mesma medida.

Dessa maneira, na figura anterior, é sempre verdade que:

α = γ

β = δ

Observe que ângulos adjacentes sempre são suplementares, pois formam “o ângulo de uma reta”, que é 180°. Agora considere os ângulos adjacentes:

α + β = 180°

γ + β = 180°

Perceba que ambas as somas resultam no mesmo valor, por isso, podemos escrever:

α + β = γ + β

α = γ + β – β

α = γ + 0

α = γ (são opostos pelo vértice)

Exemplos

1º) Na imagem a seguir, calcule a medida de cada ângulo.

Observe que γ = 60°, pois eles são opostos pelo vértice. Além disso, γ + β = 180°, logo:

γ + β = 180°

60° + β = 180°

β = 180° – 60°

β = 120°

Note, por fim, que δ = 120°, pois é oposto pelo vértice a β.

2º) Calcule o valor de cada ângulo em destaque:

Como os ângulos em destaque são opostos pelo vértice, podemos escrever:

4x + 20 = 2x + 60

4x – 2x = 60 – 20

2x = 40

x = 40
      2

x = 20

Assim, cada ângulo mede:

4x + 20 = 4·20 + 20 = 80 + 20 = 100°

Por Luiz Paulo Moreira
Graduado em Matemática

Videoaulas relacionadas: