A razão entre dois números é o quociente entre eles, e proporção é uma igualdade entre duas razões.
Razão e proporção são conceitos matemáticos que relacionam grandezas. A razão entre dois números é o quociente entre eles, e a proporção é uma igualdade entre razões. Para compreender e obter informações a partir de uma proporção, é necessário conhecer algumas propriedades.
Leia também: Como fazer operações com frações
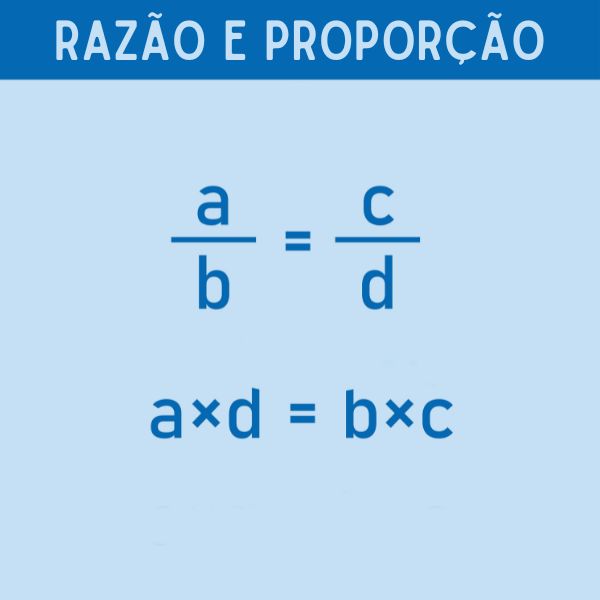
\(\frac{a}{b}\ =\ \frac{c}{d}\)
\(a\cdot d=b\cdot c\)
A razão entre dois números é o resultado da divisão entre eles, ou seja, o quociente. Considere os elementos a e b (com b≠0 ). A razão entre a e b é representada por
\(\frac{a}{b}\)
Logo:
\(\frac{a}{b}=a\div b.\).
A ordem em que os números são informados é fundamental para determinar uma razão. Assim, a razão entre a e b é diferente da razão entre b e a . No caso da razão entre b e a , representada por \(\frac{b}{a}\), temos que a≠0 .
Lembre-se de que não há divisão por zero na Matemática. Portanto, o denominador de uma razão é sempre diferente de zero.
Proporção é uma igualdade entre duas razões. Considere que a razão \(\frac{a}{b}\) é igual à razão \(\frac{c}{d}\). Isso significa que o quociente entre a e b é igual ao quociente entre c e d :
\(\frac{a}{b}\ =\ \frac{c}{d}\)
Lê-se “a está para b assim como c está para d ”.
Quando há uma relação de proporcionalidade entre grandezas, essa relação pode ser diretamente proporcional ou inversamente proporcional. Para mais detalhes sobre esse assunto, clique aqui.
Vamos conhecer algumas propriedades fundamentais da proporção.
Propriedade 1: Em uma proporção, o produto do numerador da primeira razão pelo denominador da segunda é igual ao produto do denominador da primeira razão pelo numerador da segunda.
\(\frac{a}{b}\ =\ \frac{c}{d}\ \Rightarrow a\cdot d=b\cdot c\)
Essa propriedade também é conhecida como multiplicação cruzada ou produto dos meios pelos extremos. Utilizamos essa propriedade para determinar um dos números desconhecidos de uma proporção.
Propriedade 2: Em uma proporção, a soma (ou diferença) dos numeradores e denominadores é proporcional a cada razão.
Considere a proporção \(\frac{a}{b}\ =\ \frac{c}{d}\). Assim,
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
e
\(\frac{a}{b}=\frac{c}{d}=\frac{a\ -\ c}{b\ -\ d}\)
Calcular a razão entre dois números é calcular o quociente entre eles.
Exemplos:
A razão entre 8 e 2 é 4, pois \(\frac{8}{2}=4\).
A razão entre 2 e 8 é 0,25, pois \( \frac{2}{8}=0,25\).
Em problemas relacionados a proporções, aplicamos uma propriedade para obter um dos números desconhecidos. Exemplo:
Determine o valor de x sabendo que \(\frac{9}{3}=\frac{x}{27}\).
Aplicando a propriedade 1 (multiplicação cruzada), temos que
\(9\cdot27=3\cdot x\)
\(x=\frac{243}{3}=81\)
O conceito de razão é muito utilizado no estudo de escalas cartográficas na relação entre as medidas de um mapa e as medidas reais.
Já o conceito de proporção se observa em diversas situações, como a associação entre a quantidade de itens comprados em um supermercado e o valor gasto ou o tempo gasto em uma viagem e a velocidade de movimento. Esses são, respectivamente, exemplos de grandezas diretamente proporcionais e inversamente proporcionais.
Leia também: Como calcular razões entre grandezas diferentes
Questão 1
(Enem) A taxa de urbanização de um município é dada pela razão entre a população urbana e a população total do município (isto é, a soma das populações rural e urbana).
Os gráficos apresentam, respectivamente, a população urbana e a população rural de cinco municípios (I, II, III, IV, V) de uma mesma região estadual. Em reunião entre o governo do estado e os prefeitos desses municípios, ficou acordado que o município com maior taxa de urbanização receberá um investimento extra em infraestrutura.


Segundo o acordo, qual município receberá o investimento extra?
a) I.
b) II.
c) III.
d) IV.
e) V.
Resolução
Como a taxa de urbanização de um município é a razão entre a população urbana e a população total do município, há as seguintes taxas de urbanização:
I. \(\frac{8\ 000}{12\ 000}\approx0,67\).
II. \(\frac{10\ 000}{18\ 000}\approx0,56\).
III. \(\frac{11\ 000}{16\ 000}\approx0,69\).
IV. \(\frac{18\ 000}{28\ 000}\approx0,64\).
V. \(\frac{17\ 000}{29\ 000}\approx0,59\).
Logo, o município III é o que possui a maior taxa de urbanização e, consequentemente, é o que receberá o investimento extra.
Alternativa C.
Questão 2
(UEPB — Adaptada) A razão entre a massa de uma pessoa na Terra e sua massa em Netuno é \(\frac{5}{7}\). Dessa forma, se uma pessoa tem uma massa de 60 kg na Terra, qual sua massa em Netuno?
a) 45 kg
b) 54 kg
c) 67 kg
d) 74 kg
e) 84 kg
Resolução
De acordo com o texto, tem-se a seguinte proporção:
\(\frac{5}{7}=\frac{60}{x}\)
Aplicando a propriedade 1, tem-se que:
\(5x=60\cdot7\)
\(x=84\)
Alternativa E.
Fontes:
ALMEIDA, Ricardo G. de. Razão e Proporção para além da sala de aula. Repositório Universidade Federal de Juiz de Fora (dissertação). Disponível em .
LIMA, Elon L. et al. Temas e Problemas, 3 ed. Coleção do professor de Matemática, SBM.