A área dos polígonos equivale à medida da superfície dessas figuras. Calculamos essa área usando as fórmulas de cada tipo de polígono e as medidas de seus elementos.

A área de um polígono é a medida da superfície dessa figura geométrica. Polígonos são figuras planas e fechadas formadas por segmentos de reta que se encontram nas extremidades. Triângulos, quadrados, retângulos, trapézios, losangos, pentágonos e hexágonos são alguns exemplos de polígonos.
Leia também: O que são poliedros?
\(A_{\mathrm{triângulo}}=\frac{b\cdot d}{2}\)
\(A_{\mathrm{paralelogramo}}=b\cdot h\)
\(A_{\mathrm{trapézio}}=\frac{(B+b)\cdot h}{2}\)
\(A_{\mathrm{losango}}=\frac{D\cdot d}{2}\)
A área de um polígono pode ser expressa em diferentes unidades de medida. O metro quadrado (m²) é a unidade padrão de área do Sistema Internacional de Unidades (SI) e corresponde à área de um quadrado com 1 metro de lado.
Exemplos de unidade de medida de área:
km² – quilômetro quadrado
hm² – hectômetro quadrado
dam² – decâmetro quadrado
m² – metro quadrado
dm² – decímetro quadrado
cm² – centímetro quadrado
mm² – milímetro quadrado
Como veremos mais adiante, ao aplicar uma fórmula para calcular a área de um polígono, obtemos o resultado na unidade de medida do lado do polígono elevada ao quadrado. Por exemplo, se o lado de um triângulo está indicado em centímetros (cm), ao utilizar essa medida na fórmula da área do triângulo, obtemos o resultado em centímetros quadrados (cm²).
Observação: Se a unidade de medida do lado não estiver indicada, podemos expressar a unidade de medida da área por u.a. (unidade de área).
Apótema de um polígono é o segmento perpendicular a um dos lados com extremidade no centro da figura.
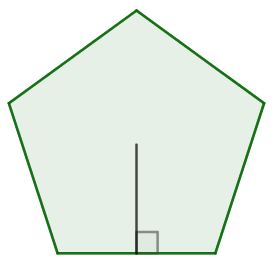
O perímetro de um polígono é a soma das medidas de seus lados.
Exemplo:
Um terreno quadrado será cercado por um muro. Se o lado do terreno mede 13 metros, qual será o comprimento do muro?
O comprimento do muro corresponde ao perímetro de um quadrado de lado com 13 metros. Portanto:
Comprimento do muro = 13+13+13+13=52
Veja também: Como calcular a área de figuras planas
Vejamos como calcular a área de alguns polígonos.
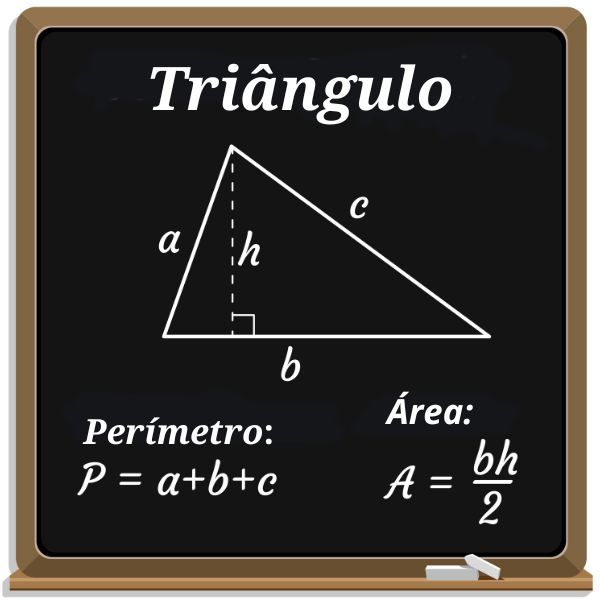
A maneira mais simples de determinar a área de um triângulo é calculando a metade do produto entre a base e a altura. Lembre-se de que a base é um dos lados do triângulo e a altura é a distância entre a base o vértice oposto.
Se a base de um triângulo mede b e a altura mede h, então a área do triângulo é dada por:
\(A_{\mathrm{triângulo}}=\frac{b\cdot d}{2}\)
Exemplo:
Qual a área de um triângulo em que base e a altura medem, respectivamente, 5 cm e 3 cm?
\(A_{\mathrm{triângulo}}=\frac{5 cm\cdot 3 cm}{2} = 7,5 cm^2\)
Observação: no caso de um triângulo equilátero, em que os três lados têm a mesma medida a, há uma expressão para a área que depende apenas de a.
\(A_{triângulo equilátero}=\frac{a^2\sqrt3}{4}\)
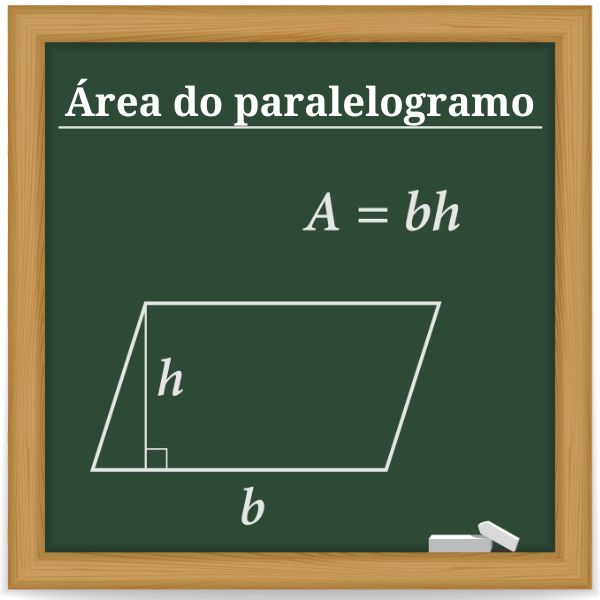
Uma das formas de encontrar a área de um paralelogramo é calcular o produto entre a base e a altura. Considera-se como base um dos lados do paralelogramo e como altura a distância entre a base e o lado paralelo.
Se a base de um paralelogramo mede b e a altura mede h, então a área do paralelogramo é dada por:
\(A_{\mathrm{paralelogramo}}=b\cdot h\)
Exemplo:
Qual a área de um paralelogramo com base b = 4,5 cm e altura h = 2 cm?
\(A_{\mathrm{paralelogramo}}=4,5cm\cdot 2 cm =9cm^2\)
Tanto o quadrado quanto o retângulo são paralelogramos. Assim, o cálculo da área desses dois polígonos é feito da mesma maneira que o cálculo da área de um paralelogramo. Como os lados adjacentes do retângulo (e do quadrado) são perpendiculares, temos que a altura desse polígono é a medida do lado adjacente à base.
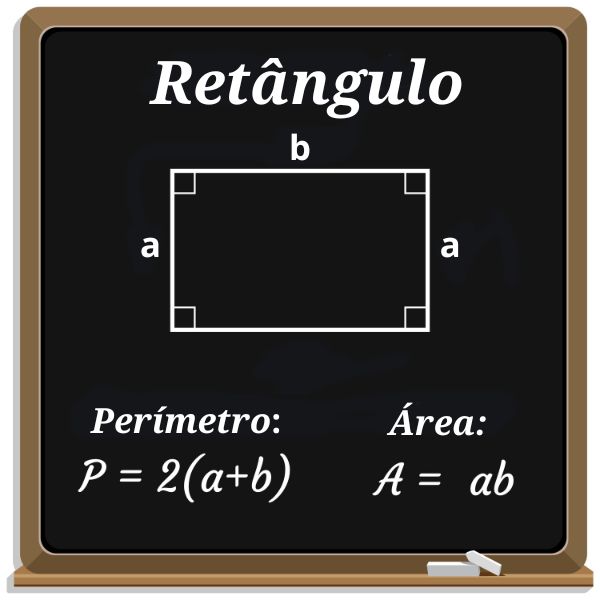
No caso específico do quadrado, como os quatro lados têm a mesma medida a, concluímos que o produto da base pela altura é igual a a2.

Se os lados adjacentes de um retângulo medem a e b , então a área do retângulo é dada por:
\(A_{\mathrm{retângulo}}=a\cdot b\)
Se os lados de um quadrado medem a, então a área do quadrado é dada por:
\(A_{\mathrm{quadrado}}=a\cdot a = a^2\)
Exemplo 1:
Um campo retangular de futebol tem 120 metros de comprimento e 90 metros de largura. Qual a área desse campo?
\(A_{\mathrm{retângulo}}=120cm\cdot90m=10.800m^2\)
Exemplo 2:
Um quadro tem o formato de quadrado com 20 centímetros de lado. Qual a área desse objeto?
\(A_{\mathrm{quadrado}}=20cm\cdot20cm=\left(20cm\right)^2=400cm^2\)
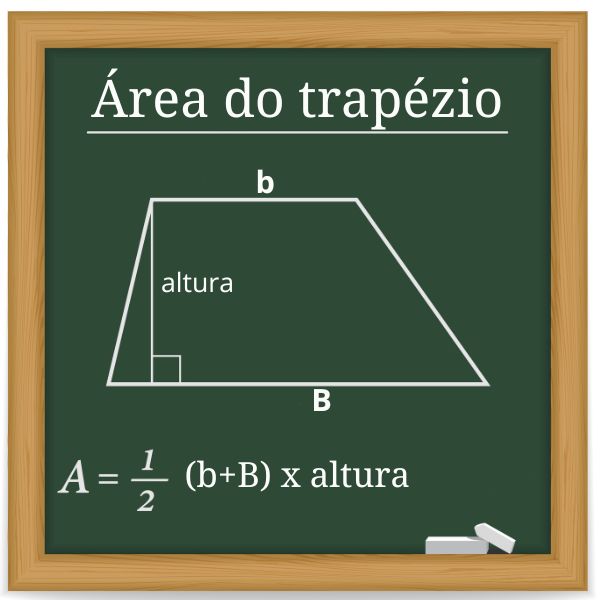
A área de um trapézio é a metade do produto entre a altura do trapézio e a soma das medidas das bases. Lembre-se de que as bases do trapézio são os lados paralelos e a altura é a distância entre as bases.
Se B é a base maior de um trapézio, b é a base menor e h é a altura, então a área do trapézio é dada por:
\(A_{\mathrm{trapézio}}=\frac{(B+b)\cdot h}{2}\)
Exemplo:
Qual a área de um trapézio com 4 cm de altura em que as bases medem 5 e 8 cm?
\(A_{\mathrm{trapézio}}=\frac{(8cm+5cm)\cdot 4cm}{2}=26cm^2\)
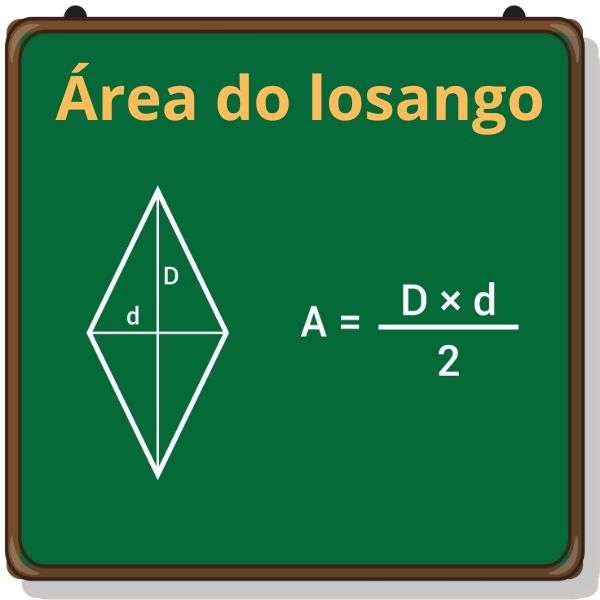
Uma das maneiras de determinar a área de um losango é calculando a metade do produto entre as diagonais. Lembre-se de que as diagonais de um losango são os segmentos que unem os vértices opostos.
Se D é a diagonal maior de um losango e d é a diagonal menor, então a área do losango é dada por:
\(A_{\mathrm{losango}}=\frac{D\cdot d}{2}\)
Exemplo:
Qual a área de um losango cujas diagonais medem 8 cm e 12 cm?
\(A_{\mathrm{losango}}=\frac{12\ cm\cdot8\ cm}{2}=96\ \mathrm{\mathrm{c}}\mathrm{m}^\mathrm{2}\)
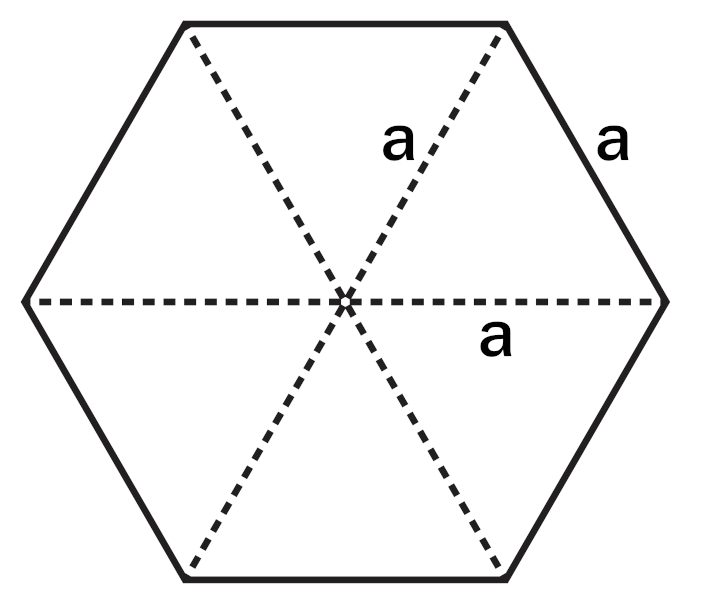
Um hexágono pode ser dividido em triângulos por segmentos que unem o centro do polígono aos vértices. Dessa forma, sua área é igual à soma das áreas dos triângulos.
No caso específico do hexágono regular, temos que os seis triângulos formados por essa divisão são equiláteros. Assim, a área de um hexágono regular é igual à soma das áreas de seis triângulos equiláteros.
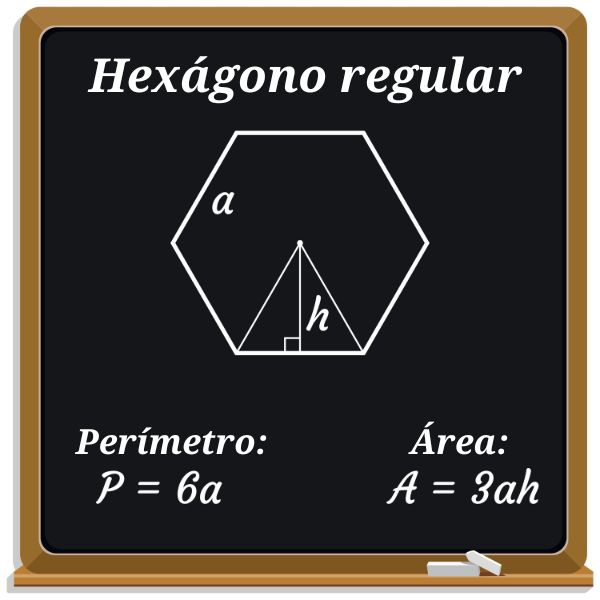
Note que a altura de cada triângulo é o apótema do hexágono. Se a é o lado de um hexágono regular e h é o apótema, então a área do hexágono é dada por:
\(A_{\mathrm{hexágono regular}}=6 \cdot\frac{a\cdot h}{2}=3\cdot a\cdot h\)
Observação: Como os seis triângulos são equiláteros, há uma expressão para a área que depende apenas do lado a do hexágono regular.
\(A_{\mathrm{hexágono regular}}=6 \cdot\frac{a^2\cdot \sqrt3}{4}\)
Exemplo:
Qual a área de um hexágono regular cujo lado mede 2 cm?
\(A_{\mathrm{hexágono regular}}=6 \cdot\frac{2^2\cdot \sqrt3}{4}=6\sqrt3\)
Para calcular a área de polígonos não convexos (côncavos), devemos segmentar o polígono em figuras com áreas conhecidas.
Exemplo:
Determine a área do polígono abaixo.
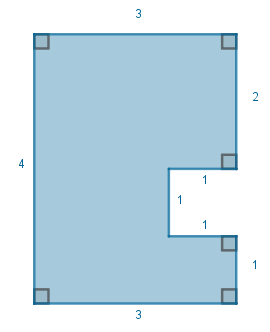
Note que esse polígono pode ser dividido em três figuras conhecidas: um retângulo com 2 de base e 4 de altura, um retângulo com 1 de base e 2 de altura e um quadrado com 1 de lado.
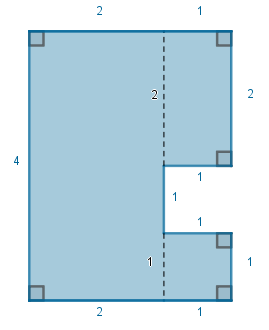
Portanto, a área do polígono será a soma das áreas das três figuras.
\(Área polígono=2⋅4+1⋅2+1^2=11\)
Saiba mais: O que são polígonos regulares?
Questão 1
A razão entre a área de um triângulo equilátero com 4 cm de lado e a área de um quadrado com 1 cm de lado é igual a
a) \(2\sqrt2\).
b) \(2\sqrt3\).
c) \(3\sqrt3\).
d) \(4\sqrt2\).
e) \(4\sqrt3\).
Resolução: alternativa E
Aplicando as fórmulas apropriadas, temos que:
\(A_{triângulo equilátero}\frac{a^2\sqrt3}{4}=\frac{4^2\sqrt3}{4}=4\sqrt3cm^2\)
\(A_{\mathrm{quadrado}}=a^2=1^2=1cm^2\)
Portanto, a razão é:
\(\frac{4\sqrt3cm^2}{1cm^2}=4\sqrt3\)
Questão 2
A altura de um trapézio com base maior, base menor e área respectivamente iguais a 15 cm, 10 cm e 75 cm² é, em centímetros, igual a:
a) 2 cm
b) 3 cm
c) 4 cm
d) 5 cm
e) 6 cm
Resolução: alternativa E
Aplicando a fórmula da área do trapézio, temos que:
\(A_{trapézio}=\frac{\left(B+b\right)\cdot h}{2}\)
\(75=\frac{\left(15+10\right)\cdot h}{2}\)
\(150=25\cdot h\)
\(h=6\ cm\)